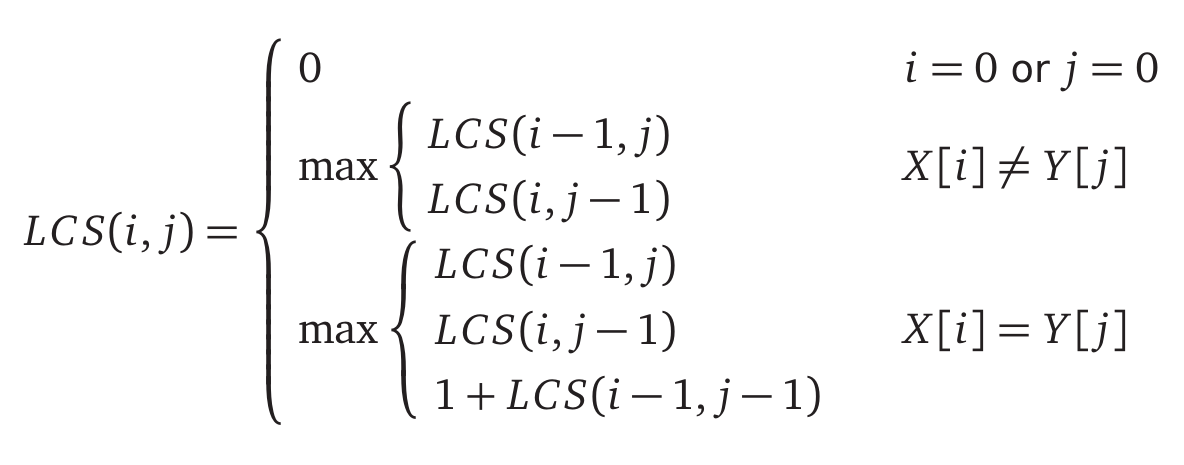Lecture 13 - Dynamic programming II

Date Pre-lecture slides Post-lecture scribbles Async video Lecture recording
October 14 2025 Lecture 13 - Dynamic programming II Lecture 13 - Dynamic programming II Lecture 13 - Dynamic programming II Lecture 13 - Dynamic programming II
 

Notes

Dynamic Programming

Steps:

  1. Develop a recursive backtracking style algorithm, $A$, for the given problem

  2. Identify the structure of the subproblems generated by $A$ on an instance, $I$, of size $n$
    • Estimate the number of different subproblems as a function of $n$ (i.e. polynomial, exponential, etc)
    • If the number of subproblems is small (polynomial) then there is typically a “clean” structure

  3. Rewrite the subproblems in a compact fashion

  4. Rewrite the recursive algorithm in terms of notation for subproblems

  5. Convert $A$ to an iterative algorithm by bottom up evaluation in an appropriate order

  6. Optimize further with data structures and/or additional ideas

Problem 1: Minimum Alignment

Background: An Alignment between two strings $X$ and $Y$ is placing one word on top of another word with potential gaps in between letters. Gaps in the first word indicate letter insertions, gaps in the second word indicate letter deletions.

Example3

Problem Statement: For each mismatch in our alignment, for some $p$ and $q$ in the alphabet, we have a Mismatch Cost $\alpha_{pq}$. For each gap in our alignment we have a Gap Cost $\delta$. Given two words $X$ and $Y$ of sizes $m$ and $n$ respectively, find the alignment with the smallest cost.

  1. The recursive backtracking algorithm is $Opt(i,j)$, the smallest alignment cost between strings $x_1 … x_i$ and $y_1 … y_j$. We can either insert, delete, or mismatch the last letter in the strings, the minimum alignment is the minimum of these options plus the minimum of the remaining alignment. This yields the following recurrence

Example3

  1. Each subproblem reduces the size of $X$ and/or $Y$ by 1, this means we will have at most $O(mn)$ different subproblems.

  2. -5. This means the recursive backtracking algorithm can be implemented by filling out an array size $m+1$x$n+1$ by initializing the base cases and computing new array elements by the minimum between previously computed elements.

EDIST(A[1..m],B[1..n])
  int M[0..m][0..n]
  for i ← 1 to m
     M[i][0] ← i*δ
  for j ← 1 to n
     M[0][j] ← j*δ
  for i ← 1 to m
     for j ← 1 to n
        M[i][j] ← min{COST[A[i]][B[j]]+M[i-1][j-1],δ+M[i-1][j],δ+M[i][j-1]}
  return M[m][n]

Running time is $O(mn)$. Space used is $O(mn)$.

  1. When computing an array element, the algorithm only uses the current and previous column (or row). Therefore we can store only the current and previous column (or row). Adding this change in results in space used being $O(\min(m,n))$.

Problem 2: Longest Common Subsequence

Problem Statement: Find the longest common subsequence between two strings, $X$ and $Y$.

  1. The recursive backtracking algorithm is $LCS(i,j)$, the longest common subsequence between strings $x_1 … x_i$ and $y_1 … y_j$. We can either choose to skip the last letter of $X$, skip the last letter of $Y$ or, if the last letters are the same, include the letters in the subsequence. This yields the following recurrence

Example3

  1. Each subproblem reduces the size of $X$ and/or $Y$ by 1, this means we will have at most $O(mn)$ different subproblems.

  2. -5. This means the recursive backtracking algorithm can be implemented by filling out an array size $m+1$x$n+1$ by initializing the base cases and computing new array elements by the minimum between previously computed elements.

LCS(A[1..m],B[1..n])
  int M[0..m][0..n]
  for i ← 1 to m
     M[i][0] ← 0
  for j ← 1 to n
     M[0][j] ← 0
  for i ← 1 to m
     for j ← 1 to n
        K ← max{M[i-1][j],M[i][j-1]}
        M[i][j] ← K
        if A[i]=B[j]
           M[i][j] ← max{K,1+M[i-1][j-1]}
  return M[m][n]

Running time is $O(mn)$. Space used is $O(mn)$.

  1. This problem can be formulated as the problem in example 1. Set the Mismatch Cost for two different letters is set to $+\infty$ and set to $1$ for two identical letters. Set the Gap Cost to $1$. The result is that the alignment will never mismatch two different letters so the longest common subsequence is the minimum alignment cost minus the number of gaps.

Even more DP problems!

Our very own Hamza Husain has dedicated himself to giving you even more DP problems for practice:

Relevent LeetCode Practice (by Tristan Yang)

  1. LeetCode 72 — Edit Distance (Hard)
    • Relevance: The canonical DP problem (Levenshtein distance). It directly uses the lecture’s insert/delete/replace recurrence.
    • ECE 374 Process: Let $dp[i][j]$ be the edit distance between the first $i$ characters of string A and the first $j$ characters of string B. The recurrence is: $dp[i][j] = \min\Big(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + [A_i \neq B_j]\Big)$, where the last term adds 0 if $A_i = B_j$ (no cost for match) or 1 if $A_i \neq B_j$ (cost for replace). This can be computed via memoization or bottom-up tabulation in $O(mn)$ time. (Space can be optimized to $O(\min(m,n))$ by only keeping two rows.)
    • Resource: NeetCode video on Edit Distance.
    • Takeaway: Edit distance frames string alignment as a path with three possible transitions (insert, delete, replace).
  2. LeetCode 1143 — Longest Common Subsequence (Medium)
    • Relevance: Straightforward application of the lecture’s subsequence DP. It’s a fundamental string DP that many others build on.
    • ECE 374 Process: Define $dp[i][j]$ as the length of the LCS of A’s first $i$ characters and B’s first $j$ characters. The recurrence: if $A_i = B_j$, then $dp[i][j] = dp[i-1][j-1] + 1$; otherwise $dp[i][j] = \max(dp[i-1][j], dp[i][j-1])$. Fill this 2D table row-by-row or column-by-column. This problem is closely related to edit distance and other sequence alignment tasks.
    • Resource: NeetCode video on LCS.
    • Takeaway: LCS reveals the optimal substructure in overlapping sequences; edit distance is a complementary problem where mismatches incur a cost instead of breaking sequence continuity.
  3. LeetCode 300 — Longest Increasing Subsequence (Medium)
    • Relevance: Illustrates a simple 1D DP recurrence for sequences (as in the lecture) and also introduces an optimization.
    • ECE 374 Process: A straightforward DP: $dp[i] = 1 + \max{dp[j] : j < i, A[j] < A[i]}$ (if no such $j$, then $dp[i]=1$). This yields an $O(n^2)$ solution. An optimized approach uses a greedy strategy with binary search to achieve $O(n \log n)$ time.
    • Resource: NeetCode video on LIS (covering both DP and the greedy+binary search method).
    • Takeaway: LIS highlights how a DP over a single sequence can sometimes be improved with greedy methods and specialized data structures, although the classic DP is easier to implement and reason about.
  4. LeetCode 139 — Word Break (Medium)
    • Relevance: Matches the lecture’s string segmentation problem (splitting a string into valid dictionary words).
    • ECE 374 Process: Use a boolean DP over the prefix of the string: let $dp[i]$ be true if the substring $s[0..i-1]$ (length $i$ prefix) can be segmented into valid words. Then $dp[i]$ is true if there exists some $j < i$ such that $dp[j]$ is true and $s[j:i]$ (the substring from $j$ to $i-1$) is in the dictionary. Solve with memoized recursion or iterative loops.
    • Resource: NeetCode video on Word Break.
    • Takeaway: Using DP on string prefixes combined with dictionary membership efficiently solves segmentation problems that would be exponential with naive recursion.

Supplemental Problems

Additional Resources

Contributors

Nicholas Bampton
Nicholas Bampton

Site created by Nickvash Kani using the backend from the Mathematical Language Processing Group website.
Electrical and Computer Engineering Department at the University of Illinois at Urbana-Champaign