Lecture 18 - Minimum spanning trees (MSTs)

Minimum Spanning Trees

Definition

• Input : Connected graph G = (V, E) with edge costs
• Goal : Find T $\subseteq$ E such that (V, T) is connected and total cost of all edges in T is smallest. T is then the minimum spanning tree (MST) of G.

Example:

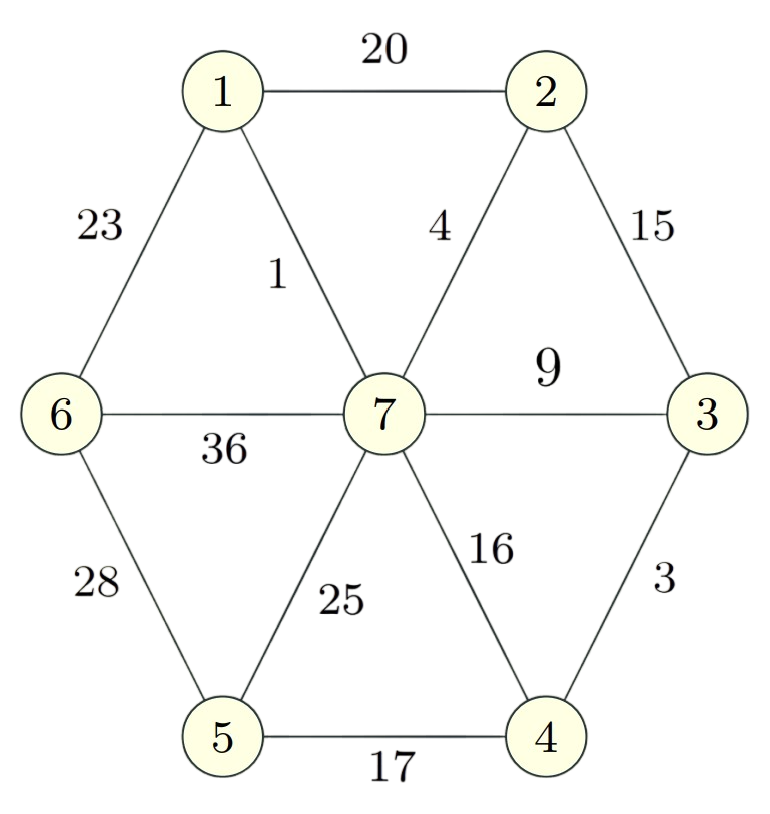
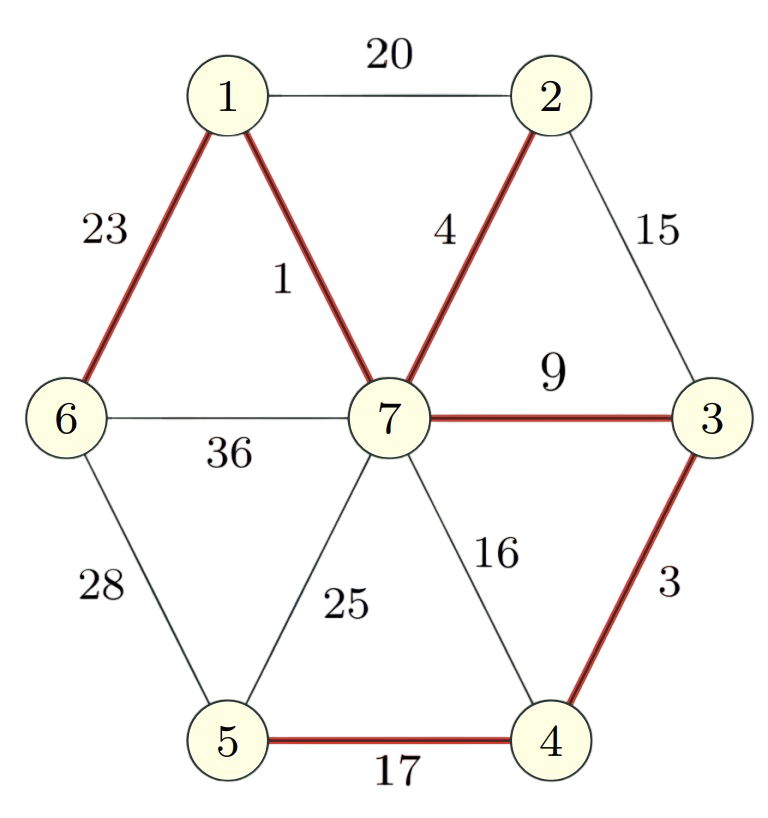
Applications

• Network Design
• Designing networks with minimum cost but maximum connectivity
• Approximation algorithms
• Can be used to bound the optimality of algorithms to approximate Traveling Salesman Problem, Steiner Trees,etc.
• Cluster Analysis

Basic Properties

• Tree = undirected graph in which any two vertices are connected by exactly one path.
• Tree = a connected graph with no cycles.
• Subgraph H of G is spanning for G, if G and H have same connected components.
• A graph G is connected $\Longleftrightarrow$ it has a spanning tree.
• Every tree has a leaf (i.e., vertex of degree one).
• Every spanning tree of a graph on n nodes has n − 1 edges.

Cuts

Given a graph G = (V, E), a cut is a partition of the vertices of the graph into two sets (S, V \ S).

• Edges having an endpoint on both sides are the edges of the cut.
• A cut edge is crossing the cut.

• (S, V \ S) = {uv $\in$ E

  u $\in$ S, v $\in$ V \ S}.

Safe and Unsafe edges

Safe edge

• Definition: An edge e = (u, v) is a safe edge if there is some partition of V into S and V \ S and e is the unique minimum cost edge crossing S (one end in S and the other in V \ S).
• So, every cut identifies one safe edge, the cheapest edge in the cut.
• Note that an edge e may be a safe edge for many cuts.
• For example: In the below graph, the edge marked in red is a safe edge in the cut (S, V\S)

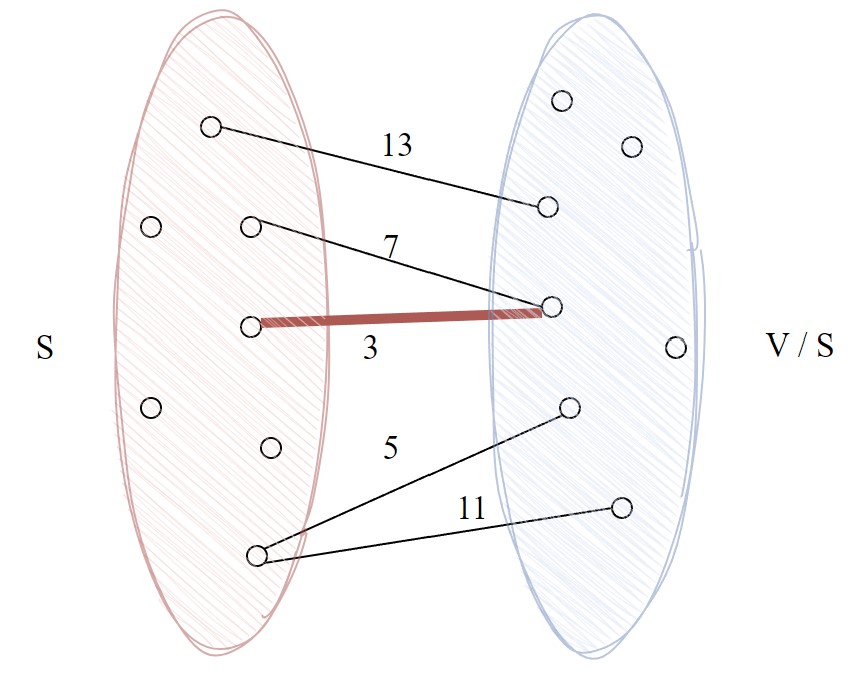
Unsafe edge

• Definition: An edge e = (u, v) is an unsafe edge if there is some cycle C such that e is the unique maximum cost edge in C.
• So, every cycle identifies one unsafe edge, the most expensive edge in the cycle.
• Example :

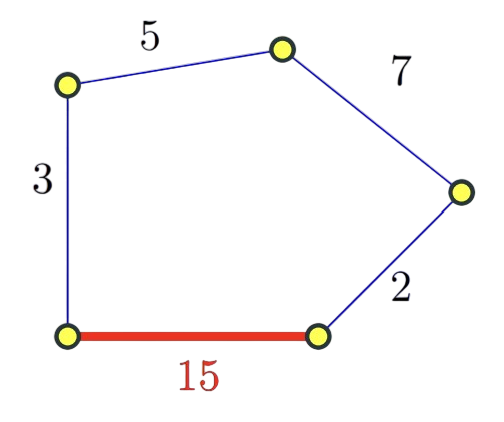
• If edge costs are distinct then every edge is either safe or unsafe

Spanning tree properties

• If e is a safe edge then every minimum spanning tree contains e.
• Suppose e = (v,w) is not in MST T and e is min weight edge in cut (S, V \ S). Assume v ∈ S. Then, T’ = (T \ {e’}) $\cup$ {e} is a spanning tree.
• The safe edges form the MST
  • Let G be a connected graph with distinct edge costs, then the set of safe edges does not contain a cycle.
  • Let G be a connected graph with distinct edge costs, then set of safe edges form the unique MST of G.
• The unsafe edges are not in the MST
  • If e is an unsafe edge then no MST of G contains e.

Algorithms

• Borůvka’s Algorithm

  T is ∅ (* T will store edges of a MST *)
  while T is not spanning do
    X ← ∅
    for each connected component S of T do
        add to X the cheapest edge between S and V \ S
    Add edges in X to T
  return the set T
  

  Running time: O(m log n) time

• Kruskals Algorithm

  Kruskal_ComputeMST
    Initially E is the set of all edges in G
    T is empty (* T will store edges of a MST *)
    while E is not empty do
        choose e ∈ E of minimum cost
        if (T ∪ {e} does not have cycles)
            add e to T
    return the set T
  

  Running time: O(m log m) + O(mn) = O(mn)

• Prim’s Algorithm

  Prim_ComputeMST
    E is the set of all edges in G
    S = {1}
    T is empty (* T will store edges of a MST *)
    while S 6= V do
        pick e = (v,w) ∈ E such that
            v ∈ S and w ∈ V \ S
            e has minimum cost
        T = T ∪ e
        S = S ∪ w
    return the set T
  

  Running time: O(nm)

• Prim’s Algorithm using Priority Queues

  Prim_ComputeMSTv3
    T ← ∅, S ← ∅, s ← 1
    ∀v ∈ V (G) : d(v) ← ∞, p(v) ← Nil
    d(s) ← 0
    while S 6= V do
        v = arg min u∈ V\S d(u)
        T = T ∪ {vp(v)}
        S = S ∪ {v}
        for each u in Adj(v) do
            d(u) ← min {d(u), c(vu)}
            if d(u) = c(vu) then
                p(u) ← v
    return T
  

Relevent LeetCode Practice (by Tristan Yang)

1. LeetCode 1584 — Min Cost to Connect All Points (Medium)
   • Relevance: It’s a pure MST problem on a complete graph of points with Manhattan distance weights. Great for demonstrating Prim’s vs Kruskal’s approaches and complexity considerations (dense graph).
   • ECE 374 Process: Model as complete graph with Manhattan distance weights. Use Prim’s algorithm: start from arbitrary point, maintain minimum edge weights to growing MST, extract-min and update keys. Implement in $O(n^2)$ time using array or $O(m \log n)$ with min-heap. Alternatively use Kruskal’s: sort all edges by weight, use Union-Find to connect components, stop after $n-1$ edges added.
   • Resource: LeetCode editorial for Min Cost to Connect All Points.
   • Takeaway: The MST total cost is invariant of the starting node. Prim’s and Kruskal’s are two greedy methods to find MSTs. The cut property guarantees that the smallest edge crossing any cut is safe to include (underpins both algorithms).
2. LeetCode 1135 — Connecting Cities With Minimum Cost (Medium)
   • Relevance: A textbook example of Kruskal’s algorithm with a graph given by a list of edges (usually sparser than the complete graph in problem 1584).
   • ECE 374 Process: Sort the given edges by weight. Iterate through them in increasing order and use DSU to keep track of components. Union the endpoints of an edge if they are currently in different components (include that edge in the MST). Stop when you’ve added $n-1$ edges or if you run out of edges before fully connecting (then it’s impossible to connect all cities).
   • Resource: LeetCode editorial for Connecting Cities With Minimum Cost.
   • Takeaway: Kruskal’s correctness comes from the cut property: the cheapest edge that connects two separate components is always part of some MST. Using DSU, we implement this efficiently in $O(m \log m)$ time (sorting edges dominates).
3. LeetCode 684 — Redundant Connection (Medium)
   • Relevance: This problem uses DSU to detect cycles by processing edges one by one, effectively mirroring the cycle-detection step in Kruskal’s algorithm.
   • ECE 374 Process: Start with $n$ isolated nodes. For each edge, check if its two endpoints are already in the same component via DSU. If not, union them (connect the components); if yes, that edge would create a cycle and is therefore the redundant one (return it). This is exactly how Kruskal “skips” edges that would form a cycle.
   • Resource: LeetCode editorial for Redundant Connection.
   • Takeaway: Union-Find is a powerful tool for cycle detection in an undirected graph. It underpins Kruskal’s MST algorithm by efficiently determining whether adding an edge will form a cycle.

Supplemental Problems

• LeetCode 1319 — Number of Operations to Make Network Connected
  A DSU connectivity problem: given a graph with n nodes, determine how many extra edges are needed to make it connected. Union all given edges; count components. If there are $c$ components and at least $c-1$ spare edges (edges beyond $n-1$), answer is $c-1$ (connect components); otherwise, it’s impossible (-1).

• LeetCode 1202 — Smallest String With Swaps
  Uses DSU in a non-weight context: union indices that can be swapped; each connected component of indices can have its characters sorted independently to achieve the lexicographically smallest result.

• LeetCode 721 — Accounts Merge
  Another DSU grouping application: union all email addresses that belong to the same person (if two accounts share an email, they’re connected). Then collect emails per connected component and sort them for the merged account output.

• LeetCode 1631 — Path With Minimum Effort
  Can be solved by binary search + BFS, but also via MST: consider each cell as a node and edges weighted by the absolute height difference. The minimum effort to connect start to end equals the minimum possible “maximum edge” on a path, which is given by the MST (specifically, find when start and end become connected as you add edges in increasing order of weight).

• LeetCode 261 — Graph Valid Tree
  Determine if an undirected graph is a tree (one component, exactly n-1 edges). Using DSU: union all edges, if you ever try to union two already-connected nodes, there’s a cycle. In the end, check that you used n-1 edges and have exactly one component.

• LeetCode 305 — Number of Islands II
  A dynamic connectivity problem. We add land cells one by one and need to report the number of islands after each addition. Use DSU: initially all water. Each time a new land appears, treat it as a new component and union it with any adjacent land components. Keep track of the component count as it evolves.

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Chapter 7 - Minimum Spanning Trees
  • Skiena, Steven. The Algorithms Design Manual
    • Chapter 8.1 - Minimum Spanning Trees
  • Sedgewick, Robert and Wayne, Kevin. Algorithms (Forth Edition)
    • Chapter 4.3 - Minimum Spanning Trees
  • Cormen, Thomas, et al. Algorithms (Forth Edition)
    • Chapter 21 - Minimum Spanning Trees
• Jeff’s Textbook - Minimum Spanning Trees
• Sariel’s Lecture 20