Lecture 18 (Abraham) - Minimum spanning trees (MSTs)

Minimum Spanning Trees

Definition

• Input : Connected graph G = (V, E) with edge costs
• Goal : Find T $\subseteq$ E such that (V, T) is connected and total cost of all edges in T is smallest. T is then the minimum spanning tree (MST) of G.

Example:

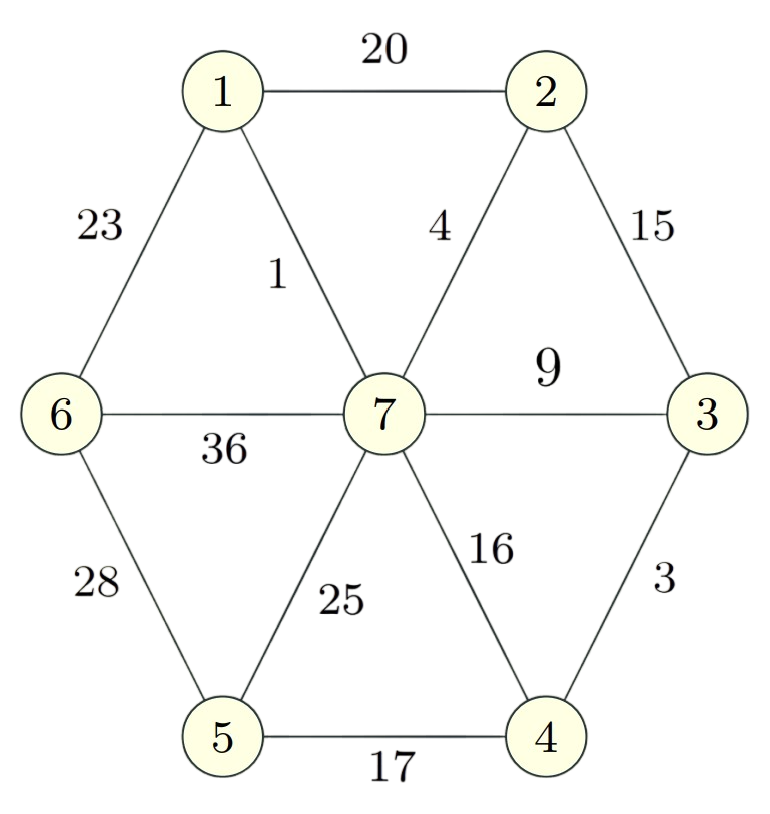
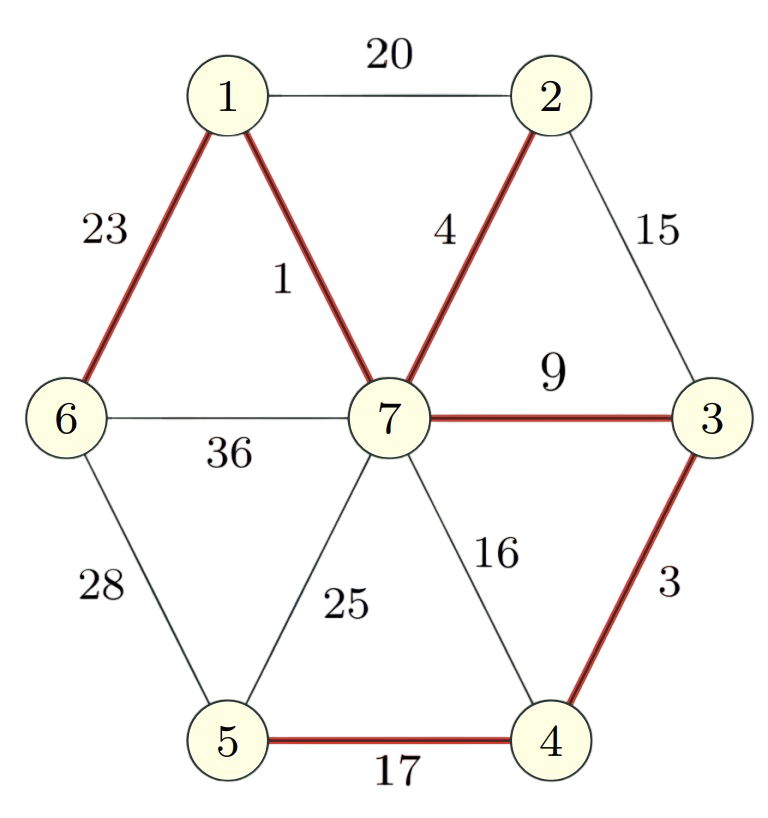
Applications

• Network Design
• Designing networks with minimum cost but maximum connectivity
• Approximation algorithms
• Can be used to bound the optimality of algorithms to approximate Traveling Salesman Problem, Steiner Trees,etc.
• Cluster Analysis

Basic Properties

• Tree = undirected graph in which any two vertices are connected by exactly one path.
• Tree = a connected graph with no cycles.
• Subgraph H of G is spanning for G, if G and H have same connected components.
• A graph G is connected $\Longleftrightarrow$ it has a spanning tree.
• Every tree has a leaf (i.e., vertex of degree one).
• Every spanning tree of a graph on n nodes has n − 1 edges.

Cuts

Given a graph G = (V, E), a cut is a partition of the vertices of the graph into two sets (S, V \ S).

• Edges having an endpoint on both sides are the edges of the cut.
• A cut edge is crossing the cut.

• (S, V \ S) = {uv $\in$ E

  u $\in$ S, v $\in$ V \ S}.

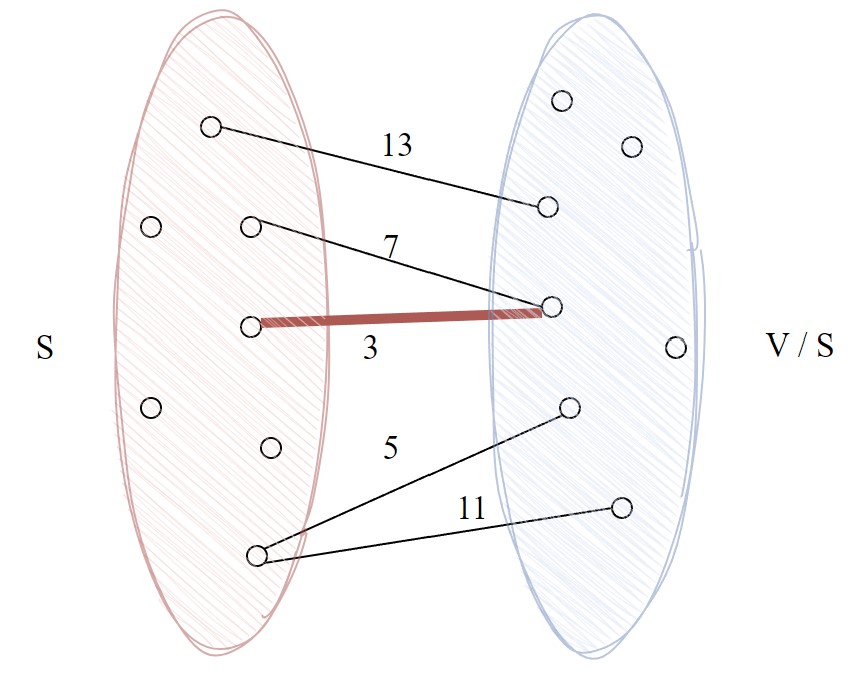
Safe and Unsafe edges

Safe edge

• Definition: An edge e = (u, v) is a safe edge if there is some partition of V into S and V \ S and e is the unique minimum cost edge crossing S (one end in S and the other in V \ S).
• So, every cut identifies one safe edge, the cheapest edge in the cut.
• Note that an edge e may be a safe edge for many cuts.
• For example: In the below graph, the edge marked in red is a safe edge in the cut (S, V\S)

Unsafe edge

• Definition: An edge e = (u, v) is an unsafe edge if there is some cycle C such that e is the unique maximum cost edge in C.
• So, every cycle identifies one unsafe edge, the most expensive edge in the cycle.
• Example :

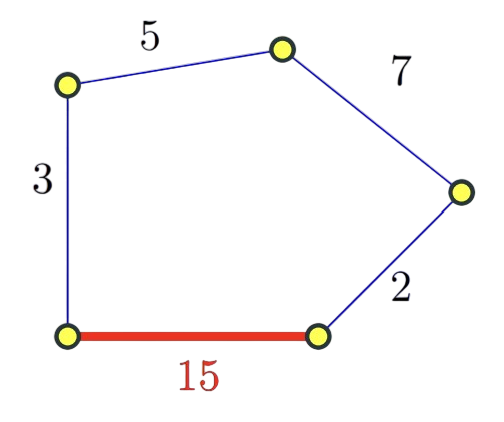
• If edge costs are distinct then every edge is either safe or unsafe

Spanning tree properties

• If e is a safe edge then every minimum spanning tree contains e.
• Suppose e = (v,w) is not in MST T and e is min weight edge in cut (S, V \ S). Assume v ∈ S. Then, T’ = (T \ {e’}) $\cup$ {e} is a spanning tree.
• The safe edges form the MST
  • Let G be a connected graph with distinct edge costs, then the set of safe edges does not contain a cycle.
  • Let G be a connected graph with distinct edge costs, then set of safe edges form the unique MST of G.
• The unsafe edges are not in the MST
  • If e is an unsafe edge then no MST of G contains e.

Algorithms

• Borůvka’s Algorithm

  T is ∅ (* T will store edges of a MST *)
  while T is not spanning do
    X ← ∅
    for each connected component S of T do
        add to X the cheapest edge between S and V \ S
    Add edges in X to T
  return the set T
  

  Running time: O(m log n) time

• Kruskals Algorithm

  Kruskal_ComputeMST
    Initially E is the set of all edges in G
    T is empty (* T will store edges of a MST *)
    while E is not empty do
        choose e ∈ E of minimum cost
        if (T ∪ {e} does not have cycles)
            add e to T
    return the set T
  

  Running time: O(m log m) + O(mn) = O(mn)

• Prim’s Algorithm

  Prim_ComputeMST
    E is the set of all edges in G
    S = {1}
    T is empty (* T will store edges of a MST *)
    while S 6= V do
        pick e = (v,w) ∈ E such that
            v ∈ S and w ∈ V \ S
            e has minimum cost
        T = T ∪ e
        S = S ∪ w
    return the set T
  

  Running time: O(nm)

• Prim’s Algorithm using Priority Queues

  Prim_ComputeMSTv3
    T ← ∅, S ← ∅, s ← 1
    ∀v ∈ V (G) : d(v) ← ∞, p(v) ← Nil
    d(s) ← 0
    while S 6= V do
        v = arg min u∈ V\S d(u)
        T = T ∪ {vp(v)}
        S = S ∪ {v}
        for each u in Adj(v) do
            d(u) ← min {d(u), c(vu)}
            if d(u) = c(vu) then
                p(u) ← v
    return T
  

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Chapter 7 - Minimum Spanning Trees
  • Skiena, Steven. The Algorithms Design Manual
    • Chapter 8.1 - Minimum Spanning Trees
  • Sedgewick, Robert and Wayne, Kevin. Algorithms (Forth Edition)
    • Chapter 4.3 - Minimum Spanning Trees
  • Cormen, Thomas, et al. Algorithms (Forth Edition)
    • Chapter 21 - Minimum Spanning Trees
• Jeff’s Textbook - Minimum Spanning Trees
• Sariel’s Lecture 20