Course policies can be found on the website ecealgo.com.
Big Questions
This course is focused on answering three big questions:
- Given infinite time, how can we group problems by their “complexity” (Computability-theory)
- Given finite time, but a problem we know is computable, how fast can we solve the problem (Algorithmic design)
- Given a problem which is difficult to solve, can we infer how slow/fast we can solve it by comparing it to other known problems (Reductions)
Two types of complexity
| Computational Complexity | Algorithmic Complexity |
|---|---|
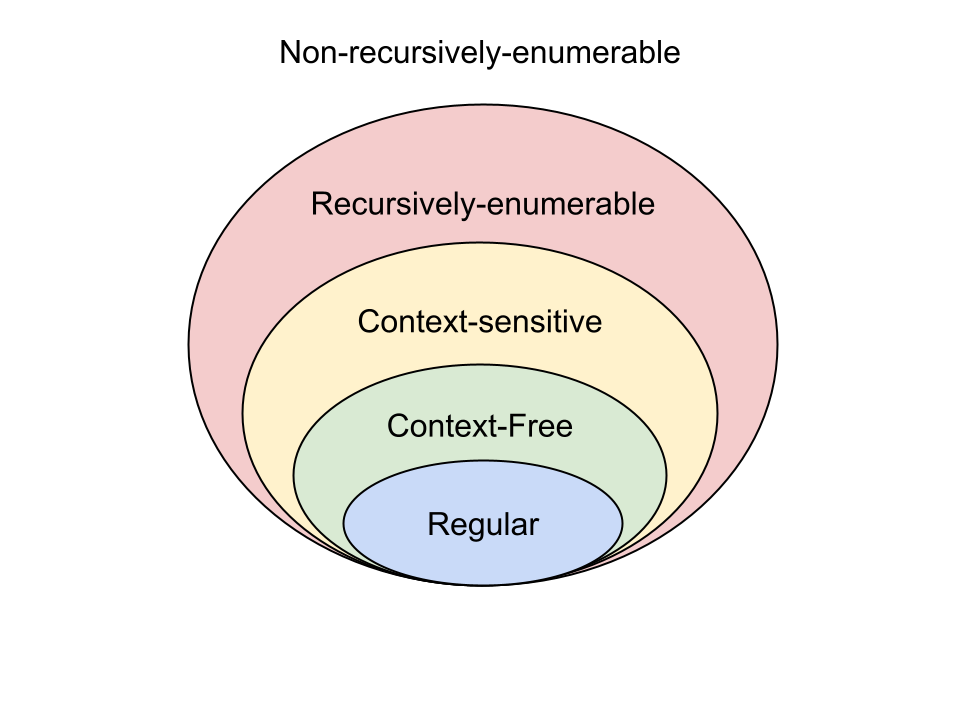 |
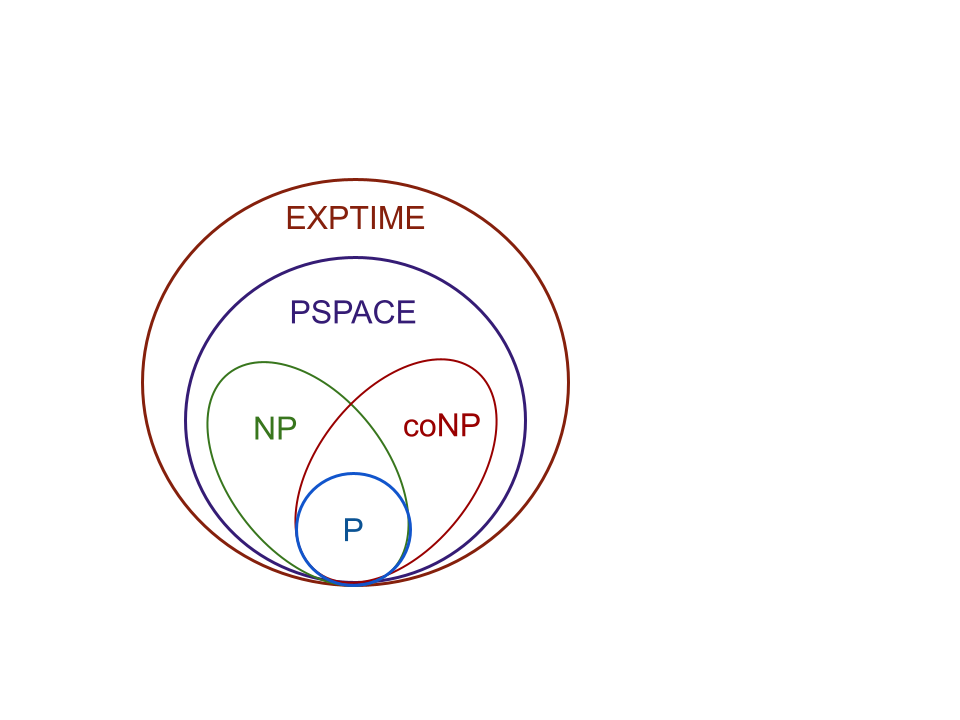 |
Why Languages?
Problems need to be represented as languages to be comparable. A language is a set of strings and each string represents and instance of the problem (a specific set of inputs and their corresponding output). For example, the problem of adding two numbers together can be represented by the language:
Problem: Multiplying two integers together
Language: \(L_{MULT2} = \begin{bmatrix} 1 \times 1|1, & 1 \times 2|2, & 1 \times 3|3, \ldots\\ 2 \times 1|2, & 2 \times 2|4, & 2 \times 3|6, \ldots \\ \vdots & \vdots & \vdots \\ n \times 1|n, & n \times 2|2n, & n \times 3|3n, \ldots \\ \end{bmatrix}\)
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Sipser, Michael. Introduction to the Theory of Computation
- Chapter 0 - Introduction - Mathematical Notation and Terminology
- Sariel’s Lecture 1
- Very cool use of induction with hydra problem

