Lecture 2 - Deterministic finite automata (DFAs)

Deterministic Finite Automata

Graphical Representation:

• DFAs are collections of states (vertices) with directed transitions (edges) that are labeled with symbols from an input set $\Sigma$
• Each state has exactly one outgoing transition for each symbol in $\Sigma$
• There is a unique state labeled the start state which is represented by an input arrow
• There is a unique set of states labeled the accepting states which are represented by double circles

  Formal Representation: Defined by 5 tuples $M = (Q, \Sigma, s, A, \delta)$

• $Q$ is a finite set of states
• $\Sigma$ is a finite set inputs
• $s \in Q$ is the start state
• $A\subset Q$ are the accepting states
• $\delta: Q \times \Sigma \rightarrow Q$ are the state transitions

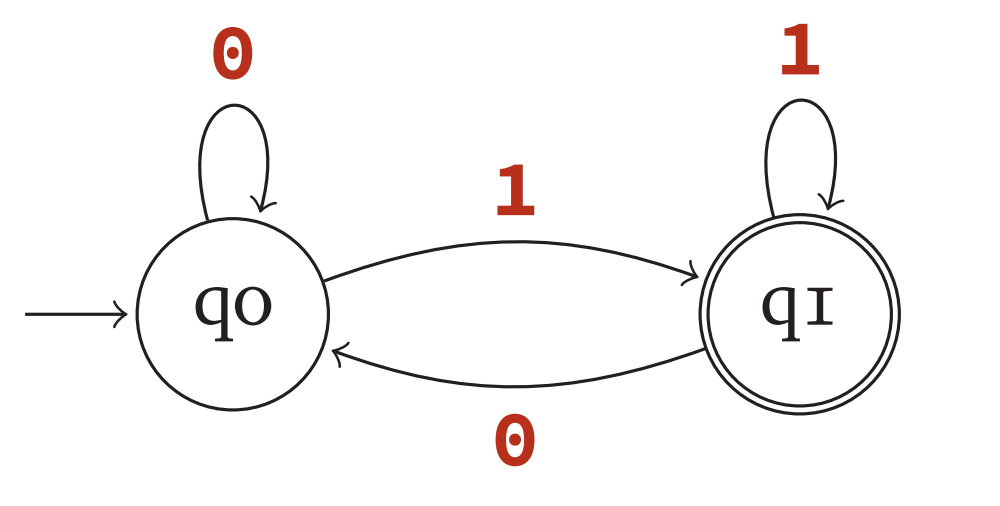
  Example:

• $Q$ = { $q_0,q_1$ }
• $\Sigma$ = { $0,1$ }
• $s$ = $q_0$
• $A$ = { $q_1$ }
• $\delta(q_0,0) = q_0$, $\delta(q_1,1) = q_1$, $\delta(q_0,1) = q_1$, $\delta(q_1,0) = q_0$

Definitions:

• DFA M accepts a string w iff the unique walk begining at the start state and sequentially inputing the symbols in w ends on an accepts state.
• The language accepted (or recognized) by a DFA is the set of strings accepted by the DFA

Formal Definitions:

• A state transition with string input w is defined by $\delta^\ast(q,w) = \delta^\ast (\delta(q,a),x)$ where $w = ax$
• The language $L(M)$ accepted by a DFA $M = (Q, \Sigma, s, A, \delta)$ is defined as $L(M)$ = { $w \in \Sigma^\ast | \delta^\ast(s,w)\in A$ }
  
  

Theorems

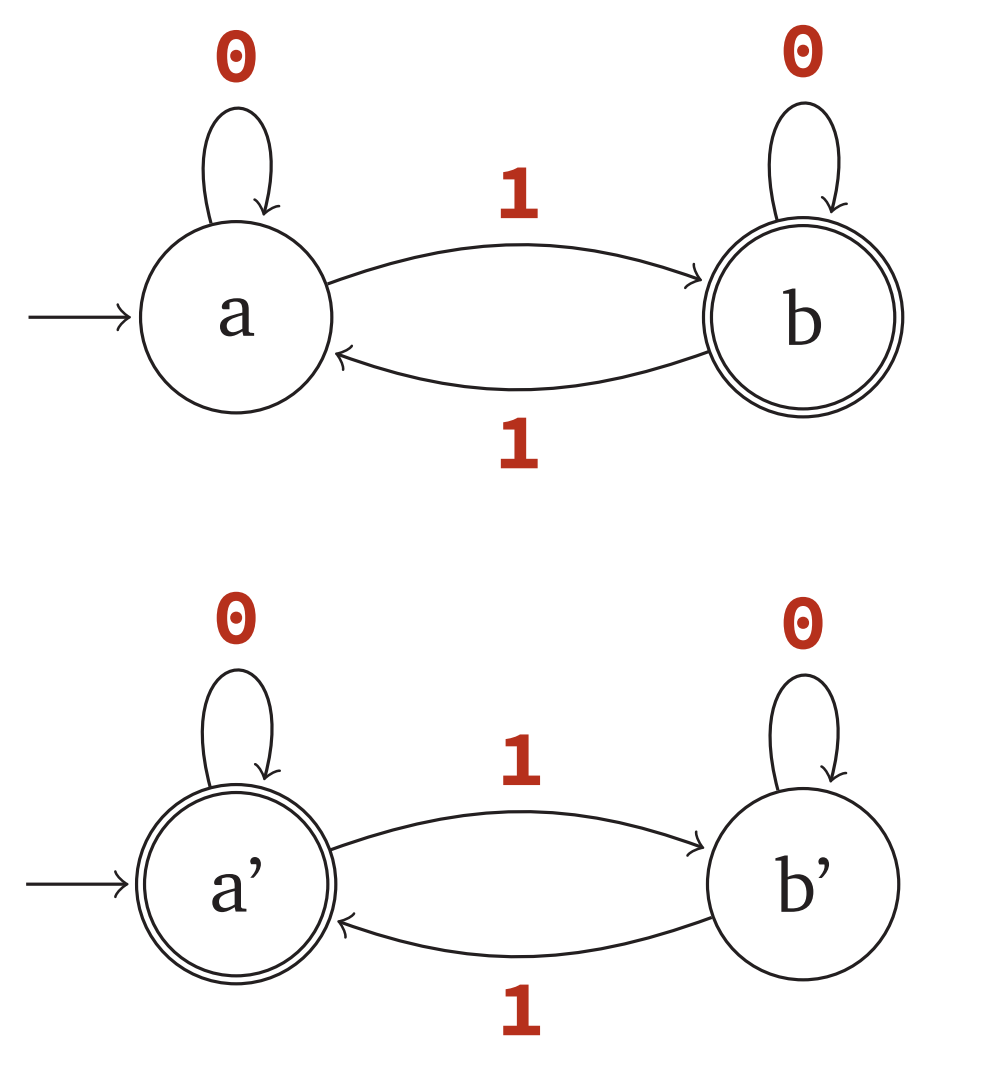
Languages accepted by DFAs are closed under compliment

If $L$ is accepted by $M_1 = (Q, \Sigma, s, A, \delta)$, then $\bar{L}$ is accepted by $M_2 = (Q, \Sigma, s, \bar{A}, \delta)$ where

• $\bar{A}$ = { $q\in Q | q \notin A$ }
  

Example:

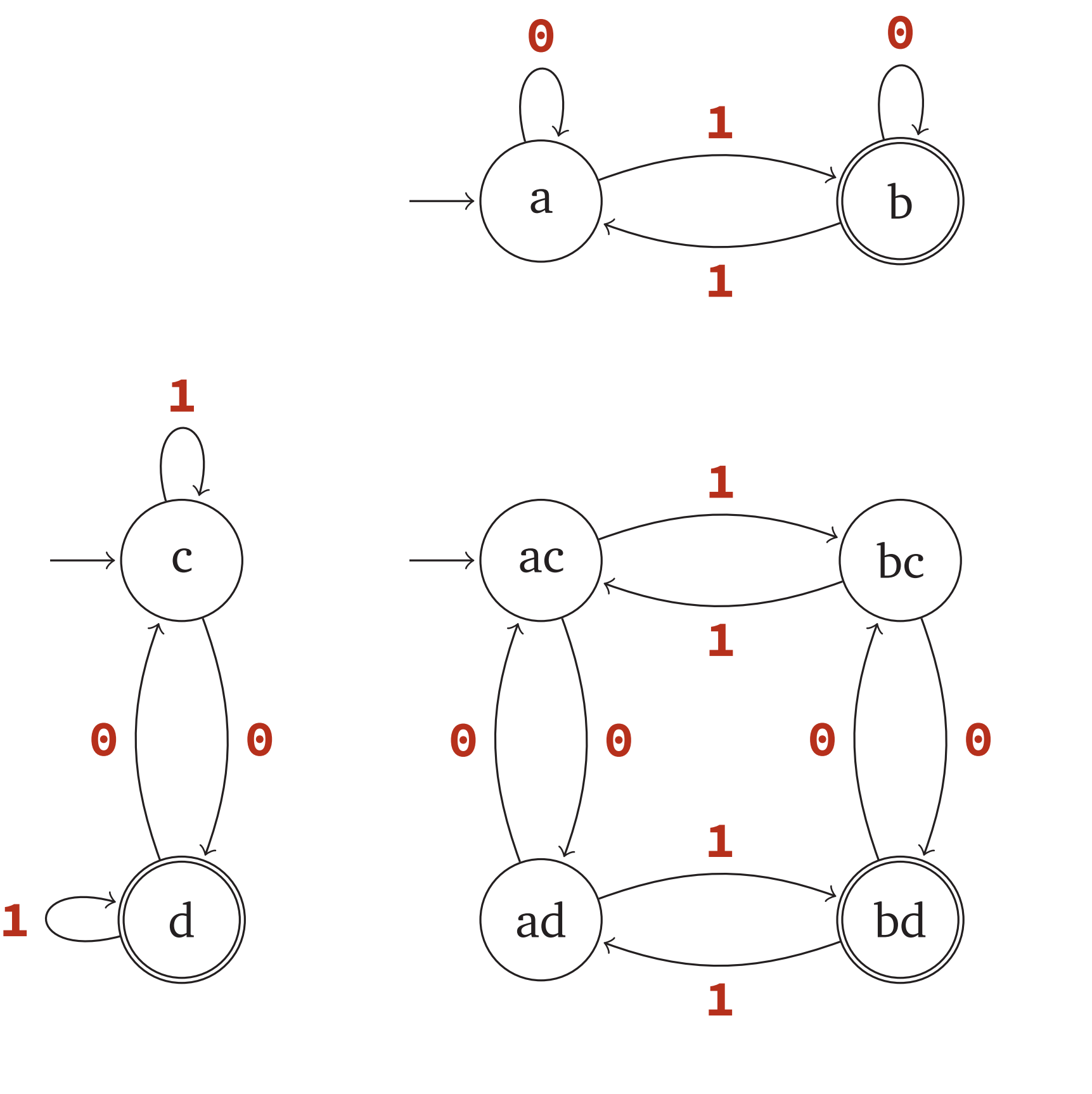
Languages accepted by DFAs are closed under intersection

If $L_1$ is accepted by $M_1 = (Q_1, \Sigma, s_1, A_1, \delta_1)$ and $L_2$ is accepted by $M_1 = (Q_1, \Sigma, s_2, A_2, \delta_2)$ then $L_1 \cap L_2$ is accepted by $M = (Q, \Sigma, s, A, \delta)$ where

• $Q$ = $Q_1 \times Q_2$
• $s$ = $(s_1,s_2)$

• $A$ = { $(q,w)\in Q

  q \in A_1 \text{ and } w \in A_2$ }

• $\delta((q,w),a) = (\delta_1(q,a),\delta_2(w,a))$
  

Example:

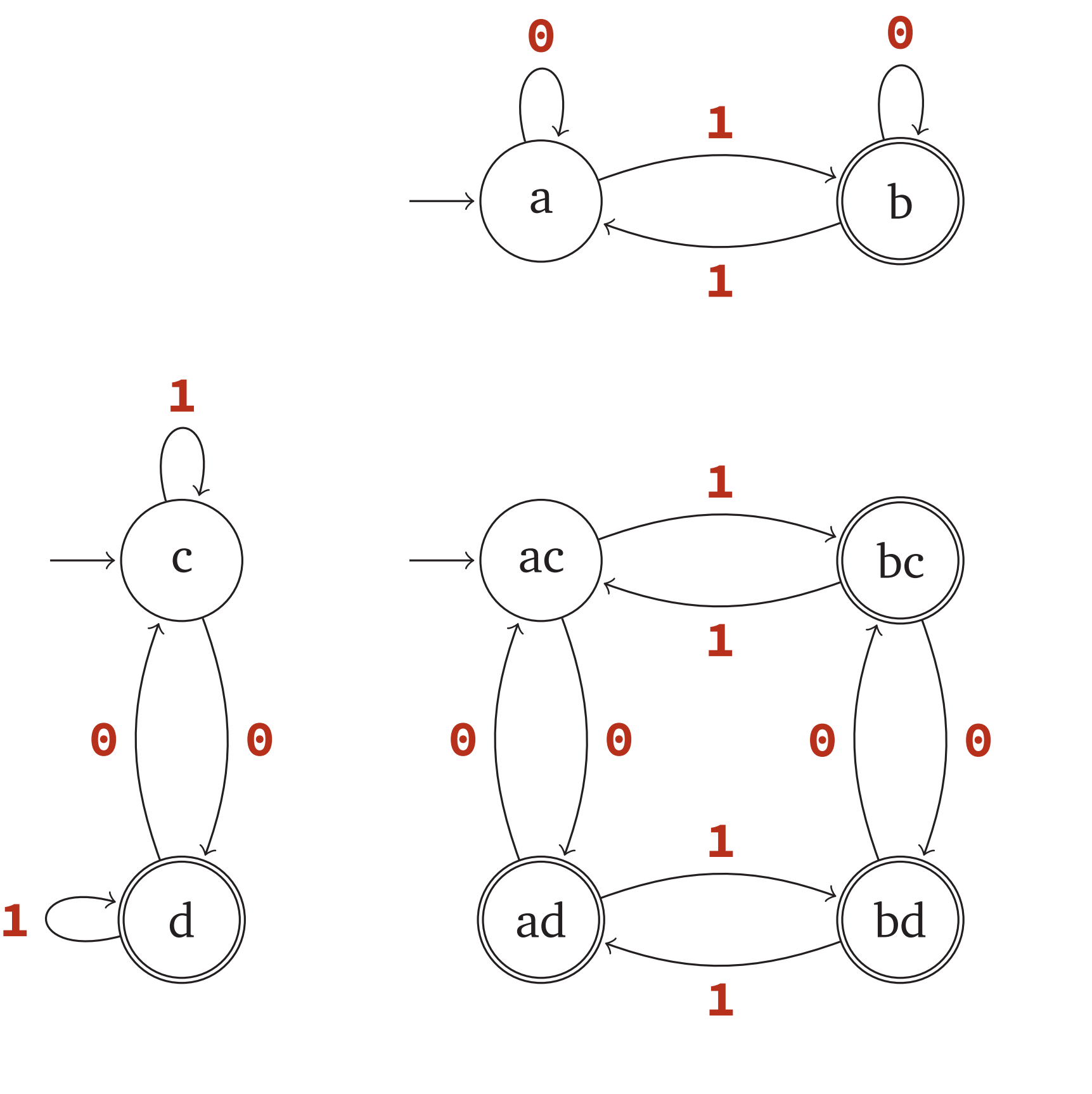
Languages accepted by DFAs are closed under union

If $L_1$ is accepted by $M_1 = (Q_1, \Sigma, s_1, A_1, \delta_1)$ and $L_2$ is accepted by $M_1 = (Q_1, \Sigma, s_2, A_2, \delta_2)$ then $L_1 \cap L_2$ is accepted by $M = (Q, \Sigma, s, A, \delta)$ where

• $Q$ = $Q_1 \times Q_2$
• $s$ = $(s_1,s_2)$

• $A$ = { $(q,w)\in Q

  q \in A_1 \text{ or } w \in A_2$ }

• $\delta((q,w),a) = (\delta_1(q,a),\delta_2(w,a))$
  

Example:

Constructing Regular Expressions from DFAs

In depth in Lecture 5

State Elimination: Slides 28-31 (55-60)

Algebraic Method: Slides 34-37 (64-68)

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Jeff’s - Notes on Finite State Automata
  • Sipser, Michael. Introduction to the Theory of Computation
    • Chapter 1 - Regular Languages - 1.1 Finite Automata
• Sariel’s Lecture 3