Context-Sensitive Language
Definition
- Context-sensitive language is a higher level language when compared to Context-Free Language.
- Context-sensitive language is a language that can be generated by some Context Sensitive Grammar and is a set of all languages that can be accepted by a Linear bounded Non-deterministic Turing machine.
Context-Sensitive Grammar
Definition
A CSG is a quadruple G = (V, T, P, S)
- V = Finite set of non-terminal symbols
- T = Finite set of terminal symbols (alphabet)
- P = Finite set of production rules
- Each production rule is represented as $\alpha$ → $\beta$
- Where $\alpha$ and $\beta$ are strings in $(V \cup T)^*$
- S = S $\in$ V is a start symbol
Example
The language L = { $a^{n} b^{n} c^{n}$ | $n \ge 1$} is a context-sensitive language.
- V = {S,A,B}
- T = {a,b,c}
- P = {S → abc | aAbc , Ab → bA , Ac → Bbcc , bB → Bb , aB → aa | aaA}
Turing Machines
Definition
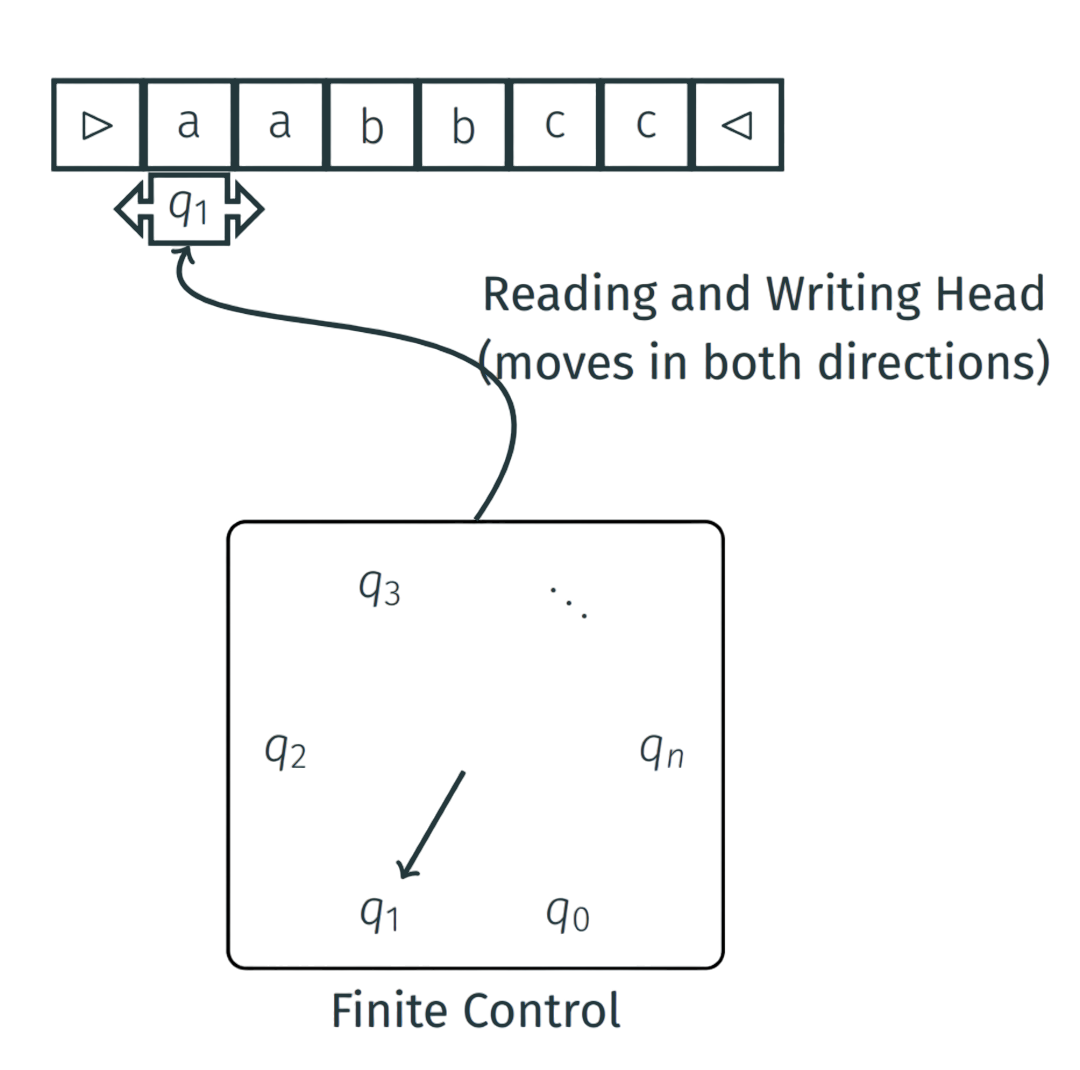
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model’s simplicity, it is capable of implementing any computer algorithm

- Input written on (infinite) one sided tape.
- Special blank characters
- Finite state control
- Every step: Read character under head, write character out, move the head right or left (or stay).
Formal definition
A Turing machine is a 7-tuple(Q, $\Sigma ,\Gamma ,\delta , q_{0}, q_{acc}, q_{rej}$)
- Q : Finite set of states
- $\Sigma$ : Finite input alphabet
- $\Gamma$ : Finite tape alphabet
- $\delta$ : Q x $\Gamma → Q$ x $\Gamma$ x {L, R, S} : Transition function.
- $q_{0}$ $\in$ Q is the initial state
- $q_{acc} \in$ Q is the accepting/final state
- $q_{rej} \in$ Q is the rejecting state
- |_| or ? : Special blank symbol on the tape
Transition Function
$\delta$ : Q x $\Gamma → Q$ x $\Gamma$ x {L, R, S}
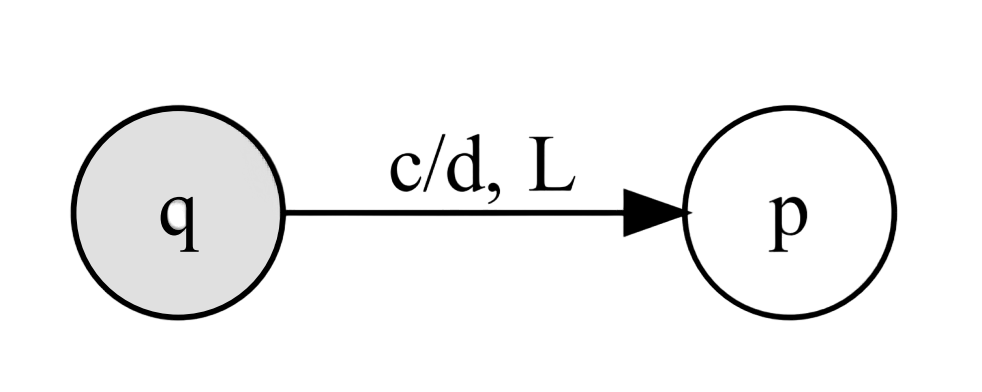
Can also be written as c → d, L
$\delta$ : (q, c) = (p, d, L)
- q : Current state.
- c : Character under tape head
- p : New state
- d : Character to write under tape head
- L : Move tape head left
Languages defined by a Turing Machine
- A language L is recursively enumerable if L is the set of strings accepted by some Turing Machine. L = {L(M) | M some Turing machine}
- A language L is recursive (decidable) if L is the set of strings accepted by some Turing Machine that halts on every input. L = {L(M) | M some Turing machine that halts on all inputs}.
Linear Bounded Automata
- (Nondeterministic) Linear bounded automata can recognize all context sensitive languages.
- Machine can non-deterministically apply all production rule to input in reverse and see if we end up with the start token.
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Sipser, Michael. Introduction to the Theory of Computation
- Chapter 3 - Turing Machines
- Sariel’s Lecture 8

