Lecture 9 - Recursion and reductions

Algorithms

Algorithmic Problem:

An algorithmic problem is to compute $f: \Sigma^\ast \rightarrow \Sigma^\ast$, a functions over the strings of a finite alphabet. We say an algorithm solves $f$ if for every input sting $\omega$ the algorithm outputs $f(\omega)$

Types of Algorithmic Problems:

• Decision Problems: Is the input a YES or a NO

  example: Given a graph $G$, for nodes $s,t$ is there a path from $s$ to $t$ in $G$.

• Search Problems: Find a solution if the input is a YES

  example: Given a graph $G$, for nodes $s,t$ find a path from $s$ to $t$ in $G$.

• Optimization Problem: Find the best solution if the input is a YES

  example: Given a graph $G$, for nodes $s,t$ find the shortest path from $s$ to $t$ in $G$.

Analysis of Algorithmic Problems:

• Does the algorithm correctly solve the problem.
• What is the asymptotic worst-case running time of the algorithm.
• What is the asymptotic worst-case space used by the algorithm.

An algorthim has an asymptotic running time of $O(f(n))$ if for every input of size $n$ the algorithm terminates after \(O(f(n))\) steps.

Reductions

A reduction from problem $A$ to problem $B$ is formatting problem $A$ in terms of problem $B$. The algorithm for $A$ uses the algorithm for $B$ as a black box.

example: Given an array $A$ of n integers, are there any duplicates in $A$.

Solving directly by comparing every element to every other element takes $O(n^2)$ running time. If we sort the array first then elements only need to be compared to adjacent elements which takes total $O(n log(n))$ running time. This is a reduction of the duplicate elements problem into the sorting problem when we use the sorting algorithm as a black box.

Types of Reductions:

Given 2 problems $C$ and $D$ where problem $C$ reduces to problem $D$

• Positive Direction: Constructing an algorithm for $C$ implies a construction of an algorithm for $D$.
• Negative Direction: If the reduction from problem $C$ to problem $D$ is “efficient”. Assuming there is no “efficient” algorithm for $C$ implies there is no “efficient” algorithm for $D$

Recursions

A recursion is a special case of reduction where the problem is reduced to a “smaller” instance of itself.

example: Tower of Hanoi, moving a tower of size $n$ from peg $0$ to peg $2$.

The problem can be generalized to move a tower of size $m$ from peg $x$ to peg $y$. Then the problem of moving a tower of size $n$ from peg 0 to peg 2 can be viewed as moving a tower of size $n-1$ from peg 0 to peg 1, then moving the bottom disk to peg 2, and finally moving the tower of size $n-1$ from peg 1 to peg 2. Therefore a general algorithm that moves a tower of size $m$ from peg $x$ to peg $y$ can be recursively implemented as the ordering/ labeling of the pegs does not impact the problem.

Running Time Analysis:

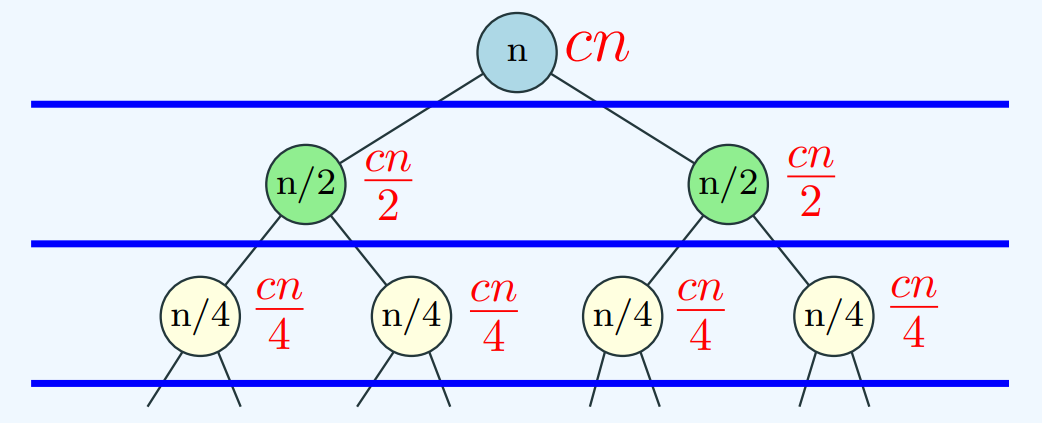
• Recursion Tree: A recurrence relation can be viewed as tree which splits at a node based on the integer constant that multiplies the recurrent function. Then the running time can be computed by looking at the running time contributed by each layer in the tree.

example: $T(n) = 2T(n/2)+cn$ split into 2 after each node but the running time contributed by each split is $cn/2$. This results in a constant amount of work done at each level. The total running time is the sum of the running times for each level. Because $n$ divides by 2 each time, there are $log(n)$ levels. This results in a total running time of $O(nlog(n))$.

• Expanding the Recurrence: Expanding the recurrence is done by replacing the recurrent function on the right side of the equation the right hand side of the equation for the smaller case.

example: $T(n) = 2T(n/2) + cn$ can be rewritten as $T(n) = 2(2T(n/4)+cn/2)+cn = 4T(n/4)+cn+cn$. This replacement can occur $log(n)$ times because $n$ divides by 2 each time. Every time the replacement occurs an extra $cn$ is added. This means the eventual expansion will be $T(n) = cn+…cn = cnlog(n)$ which has a running time of $O(nlog(n))$.

• Master Theorem for recurrence of the form $T(n) = r T(n/c) + f(n)$
  • Why does the master theorem work? by CA Ajitesh Dasaratha

Relevent LeetCode Practice (by Tristan Yang)

1. LeetCode 912 — Sort an Array (Medium)
   • Relevance: Directly implements MergeSort from the slides (split, recurse, merge) and lets you analyze
     $T(n) = 2T(n/2) + cn = \Theta(n \log n)$.
     $T(n) = 2T(n/2) + cn = \Theta(n \log n)$
     $T(n) = 2T(n/2) + cn = O(n \log n)$ via recursion trees.
   • ECE 374 Process: Write mergeSort(A[1..r]), prove merge by induction, then MergeSort by induction; argue linear work per level, $\log_2 n$ levels.
   • Resource: CLRS mergesort notes / any mergesort code walkthrough.
   • Takeaway: Divide-and-conquer + linear combine ⇒ $n \log n$.
2. LeetCode 704 — Binary Search (Easy)
   • Relevance: Matches the slide’s BinarySearch(A[a..b], x) and recurrence
     $T(n) = T(\lfloor n/2 \rfloor) + O(1) = O(\log n)$.
   • ECE 374 Process: Maintain loop/recurrence invariant on half-interval; prove termination and correctness; count steps by halving.
   • Resource: LeetCode editorial.
   • Takeaway: Halving subproblem size ⇒ logarithmic depth.
3. LeetCode 50 — Pow(x, n) (Medium)
   • Relevance: Classic recursion / self-reduction: exponentiation by squaring with
     $T(n) = T(n/2) + O(1) = O(\log n)$.
     Ties to expansion and recursion-tree reasoning.
   • ECE 374 Process: Define base cases, reduce problem to size $n/2n/2n/2$, prove by induction; compute work per level is constant.
   • Resource: NeetCode video.
   • Takeaway: Self-reduction (recursion) shrinks input geometrically.

Supplemental Problems

• LeetCode 278 — First Bad Version
  Pure binary search on search space with $O(\log n)$ halving recurrence.

• LeetCode 33 — Search in Rotated Sorted Array
  Binary search on piecewise-sorted intervals.

• LeetCode 88 — Merge Sorted Array
  Implements the merge subroutine from slides (two-pointer linear pass).

• LeetCode 875 — Koko Eating Bananas
  Another binary search on feasible answer (decision → optimization reduction).

Interesting Problems

• Why do all comparison-based sorting algorithms have to run in O(n log n)? by CA Ajitesh Dasaratha

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Chapter 1 - Recursion
  • Skiena, Steven. The Algorithms Design Manual
    • Chapter 1.5 - Modeling the Problem
    • Chapter 2.1 - The RAM Model of Computation
    • Chapter 2.2 - The Big Oh Notation
    • Chapter 2.5 - Reasoning about Efficiency
  • Sedgewick, Robert and Wayne, Kevin. Algorithms (Forth Edition)
    • Chapter 1.1 - Basic Programming Model
  • Cormen, Thomas, et al. Algorithms (Forth Edition)
    • Chapter 2.3 - Designing Algorithms
    • Chapter 4 - Divide and Conquer
    • Chapter 4.4 - The recursion tree method for solving recurrences
    • Chapter 4.5 - The master method for solving recurrences
• Sariel’s Lecture 10
• Great Reducible video on Towers of Hanoi
• Sariel’s Lecture 10