Lecture 10 - Divide and conquer and selection algorithms

Introduction to Divide and Conquer Algorithms

Divide and Conquer is a popular algorithmic paradigm used in computer science and mathematics. It is a problem-solving technique that breaks a complex problem into smaller sub-problems, solves each sub-problem independently, and then combines their solutions to obtain the solution of the original problem.

The “divide” step involves breaking the problem into smaller sub-problems, while the “conquer” step involves solving each sub-problem. Finally, the “combine” step involves merging the solutions of the sub-problems to obtain the solution of the original problem.

This approach is often used to solve problems that can be broken down into smaller, simpler sub-problems, and is frequently used in computer science for algorithm design. Divide and conquer algorithms have been used to solve a wide range of problems, including sorting, searching, matrix multiplication, and many more. The efficiency and effectiveness of divide and conquer algorithms have made them an important tool in the arsenal of computer scientists and mathematicians.

Merge Sort Algorithm

Merge Sort is a sorting algorithm that follows the Divide and Conquer paradigm. It works by recursively dividing the array into two halves until each sub-array contains only one element, and then merging the sorted sub-arrays to produce the final sorted array.

Example:

Breaking down the array into simple single element arrays:

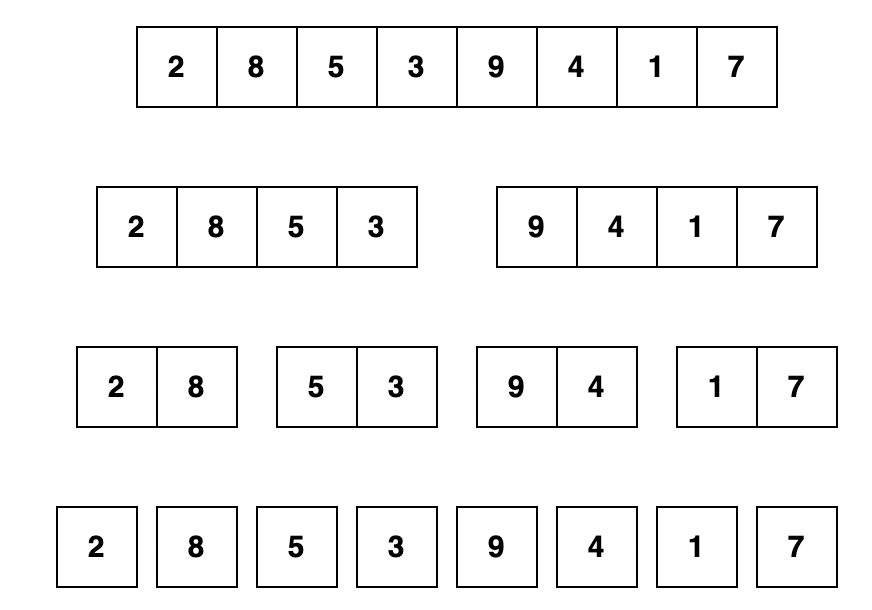
After combining the small arrays by arranging elements in proper order:

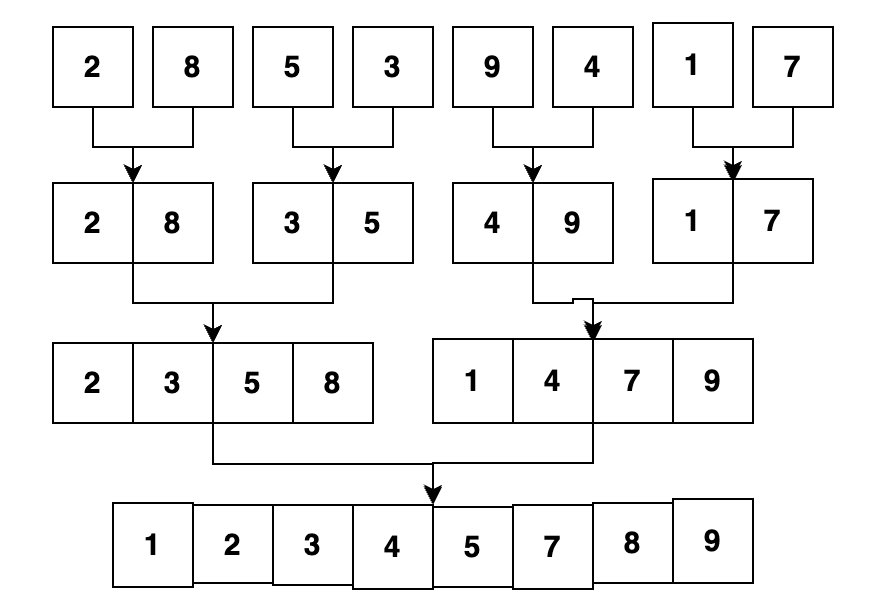
Time Complexity

The time complexity of Merge Sort is O(n logn) in the average and worst cases, where n is the number of elements in the array. The space complexity of Merge Sort is O(n).

Quick Sort Algorithm

Quick Sort is a sorting algorithm that follows the Divide and Conquer paradigm. It works by partitioning the array into three parts, based on a chosen pivot element, and recursively sorting the sub-arrays and concatenating them.

Time Complexity

The time complexity of Quick Sort depends on the choice of pivot element. In the average case, the time complexity is O(nlogn), where n is the number of elements in the array. In the worst case, where the pivot element is always chosen to be the largest or smallest element, the time complexity is O(n^2). However, Quick Sort is usually faster than other sorting algorithms in practice, because it has good cache performance and can be easily parallelized.

Quick Select Algorithm

Quickselect is a simple and efficient algorithm for finding the k-th smallest element in an unsorted array. The basic idea behind the algorithm is to use the partitioning technique from quicksort to divide the array into smaller and larger subarrays around a pivot element, and then recursively search only the subarray containing the desired element.

The algorithm has an average time complexity of O(n), where n is the size of the input array. However, the worst-case time complexity can be O(n^2), if the pivot element chosen is always the largest or smallest element in the array. This can be avoided by choosing a random or median-of-three pivot element.

Improving Worst-Case Time Complexity of Quickselect

The worst-case time complexity of the quickselect algorithm can be improved from O(n^2) to O(n) by selecting a good pivot element.

Median-of-Medians Algorithm

One way to select a good pivot element is to use the “median-of-medians” algorithm, which guarantees that the chosen pivot element is close to the true median of the subarray. The median-of-medians algorithm works by recursively dividing the subarray into groups of five elements, computing the median of each group, and then recursively computing the median of the medians until a single pivot element is found.

Relevent LeetCode Practice (by Tristan Yang)

1. LeetCode 215 — Kth Largest Element in an Array (Medium)
   • Relevance: Exactly the selection problem from the lecture; implement QuickSelect and reason about $T(n) = T(k-1) + T(n-k) + O(n)$, with worst-case $O(n^2)$. Mention the Median-of-Medians (MoM) algorithm to guarantee linear time.
   • ECE 374 Process: Partition the array into $A_{<a}, {a}, A_{>a}$ around a pivot $a$, then recurse on the relevant side. Using MoM to choose pivots yields split sizes $\le \frac{7n}{10}$, hence $T(n) \le T(n/5) + T(7n/10) + O(n) = O(n)$.
   • Resource: LeetCode editorial (Quickselect + proof sketch).
   • Takeaway: Selection = reduce problem via partitioning; MoM gives deterministic $O(n)$ solution.
2. LeetCode 4 — Median of Two Sorted Arrays (Hard)
   • Relevance: Median-finding by binary partition (divide & conquer flavor); contrasts with unsorted selection + MoM from the notes.
   • ECE 374 Process: Use two-array binary search to maintain balanced split between two sorted arrays; runs in $O(\log(\min(m,n)))$ time.
   • Resource: LeetCode editorial proof using partition invariants.
   • Takeaway: Median of two sorted arrays via partitioning = logarithmic divide & conquer.
3. LeetCode 43 — Multiply Strings (Medium)
   • Relevance: Big-integer multiplication from the notes (grade-school method $\Theta(n^2)$). Discuss how Karatsuba’s algorithm reduces 4 recursive multiplications to 3, so $T(n) = 3T(n/2) + O(n) = O(n^{\log_2 3})$.
   • ECE 374 Process: Implement the grade-school multiplication; then outline Karatsuba’s trick: $(b_L x + b_R)(c_L x + c_R)$ is computed with three recursive products instead of four.
   • Resource: CP-algorithms article on Karatsuba multiplication.
   • Takeaway: Algebraic trick ⇒ fewer recursive multiplications ⇒ better asymptotic runtime.

Supplemental Problems

• LeetCode 23 — Merge k Sorted Lists
  Ties to the pre-lecture teaser (k-way merge vs 2-way merge) and the divide-and-conquer pairing strategy.

• LeetCode 75 — Sort Colors
  Dutch National Flag problem = 3-way partitioning (same pivot-bucketing idea as Quicksort).

• LeetCode 347 — Top K Frequent Elements
  Selection-style problem: use bucket sort / heap / Quickselect partitioning to find k most frequent items.

• LeetCode 327 — Count of Range Sum
  Uses prefix sums + merge-sort-based counting (same pattern as the “Reverse Pairs” problem).

• LeetCode 315 — Count of Smaller Numbers After Self
  Another merge-sort counting problem with an identical divide-and-conquer recurrence.

• LeetCode 912 — Sort an Array (MergeSort implementation)
  Explicit two-way split vs. hypothetical k-way splits (from the teaser); useful to compare cost models of merging.

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Chapter 1 - Recursion
  • Skiena, Steven. The Algorithms Design Manual
    • Chapter 5 - Divide and Conquer
    • Chapter 17.3 - Median and Selection
  • Sedgewick, Robert and Wayne, Kevin. Algorithms (Forth Edition)
    • Chapter 2.2 - MergeSort
    • Chapter 2.3 - QuickSort
    • Chapter 2.5 - Median and order statistics
  • Cormen, Thomas, et al. Algorithms (Forth Edition)
    • Chapter 4 - Divide and Conquer
    • Chapter 14.4 - Longest Common Subsequence
• Sariel’s Lecture 11