Nondeterministic Finite Automaton(NFA)
An NFA is a finite-state automaton that can non-deterministically transition between states. Unlike a DFA, an NFA can:
- Transition without taking an input symbol, which is called $\epsilon$-transition.
- Have multiple transitions for the given source state and the input symbol.
Due to the properties described above, there can be multiple possible ways of transitioning between states given a single input string. If there exists a way to transition from the start state to an accepting state, then the NFA accepts the input string. Consider the following example of an NFA.
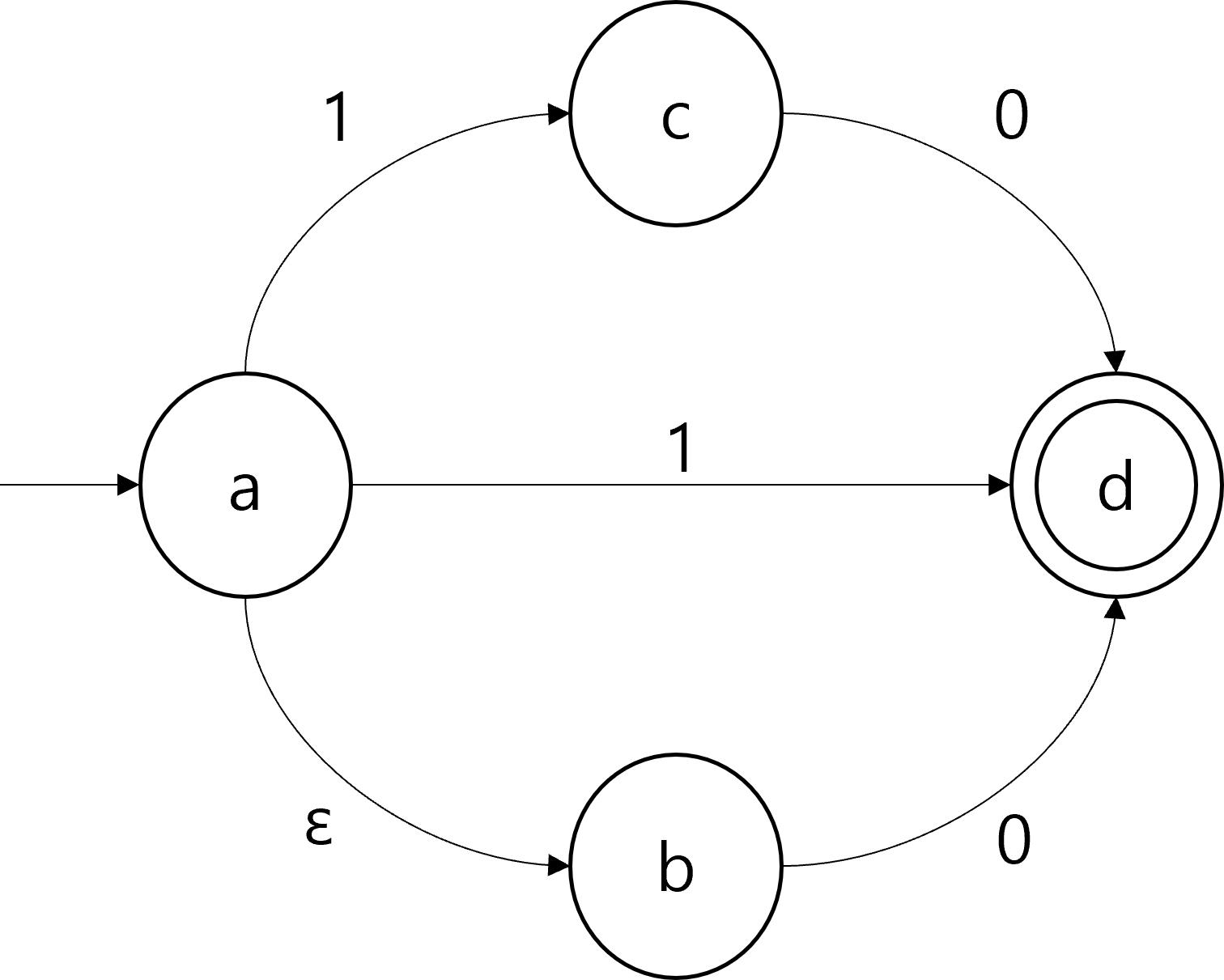
Suppose the NFA received $1$ as an input string. There exists a transition from $a$ directly to the accepting state $d$, so the NFA accepts the input $1$. For an input $0$, there is a transition leading to $d$, by taking the $\epsilon$-transition to $b$ and then to $d$. For an input $10$, the NFA can reach $d$ through the state $c$. Therefore, the NFA accepts three strings, $0$, $1$, and $10$.
Formal Definition of NFA
Formal definition of NFA is similar to that of DFA, except for the transition function. An NFA $N$ is a 5-tuple $N=(\Sigma, Q, \delta, s, A)$, which are input alphabet, states, transition function, start state, and accepting states, respectively. However, unlike DFA, the transition function $\delta:Q\times \Sigma \rightarrow 2^Q$ is a function that maps the pairs of a state and an input symbol to the power set of $Q$. This is because there can be multiple possible transitions for the given source state and the input symbol, each leading to a different state. The transition function of the example NFA above can be formally described as the following.
\[\delta(a, \epsilon)= \{ b \}\] \[\delta(a, 1)=\{c, d\}\] \[\delta(c, 0)=\{d\}\] \[\delta(b, 0)=\{d\}\]Note that not every (state, input symbol) pairs appear in the above definition. The missing pairs are implicitly mapped to the empty set $\emptyset$.
Closure properties of Regular Languages
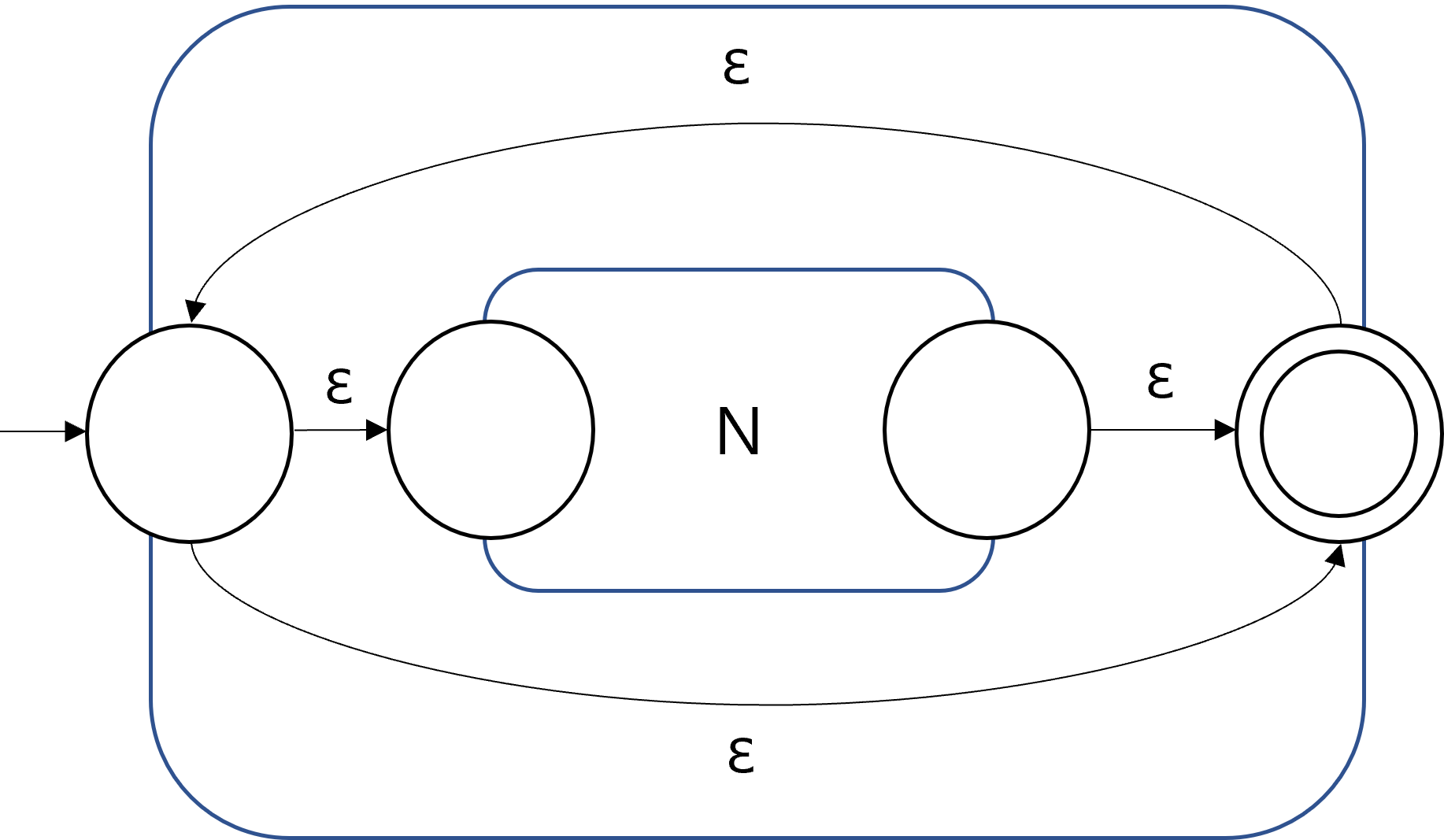
An arbitrary NFA can be transformed to have a single accepting state as appears in the following figure.
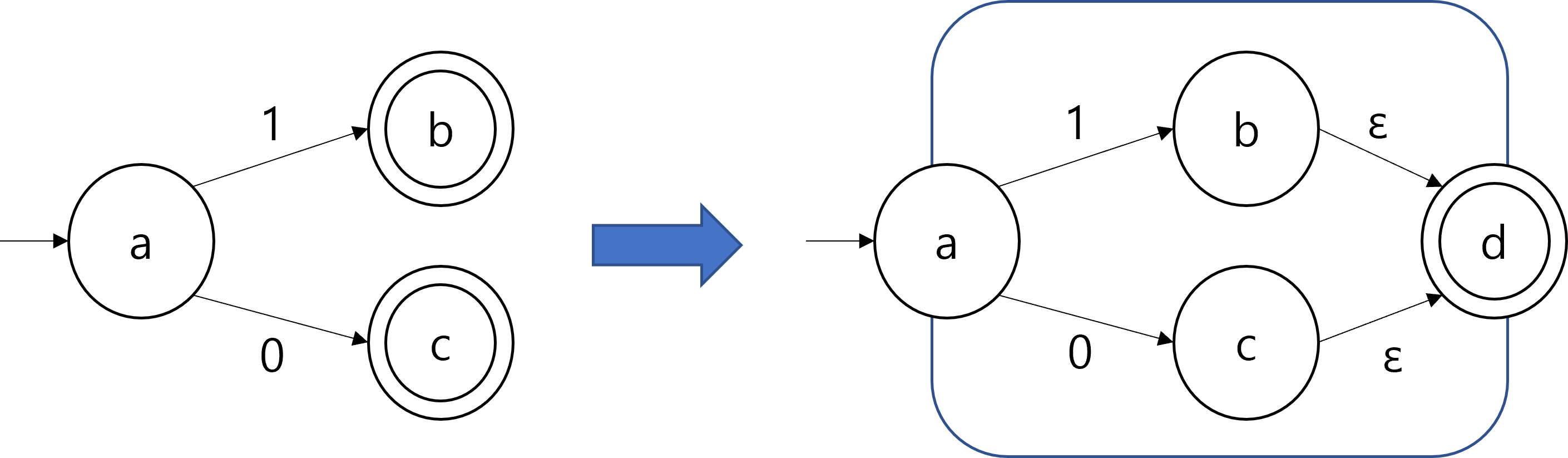
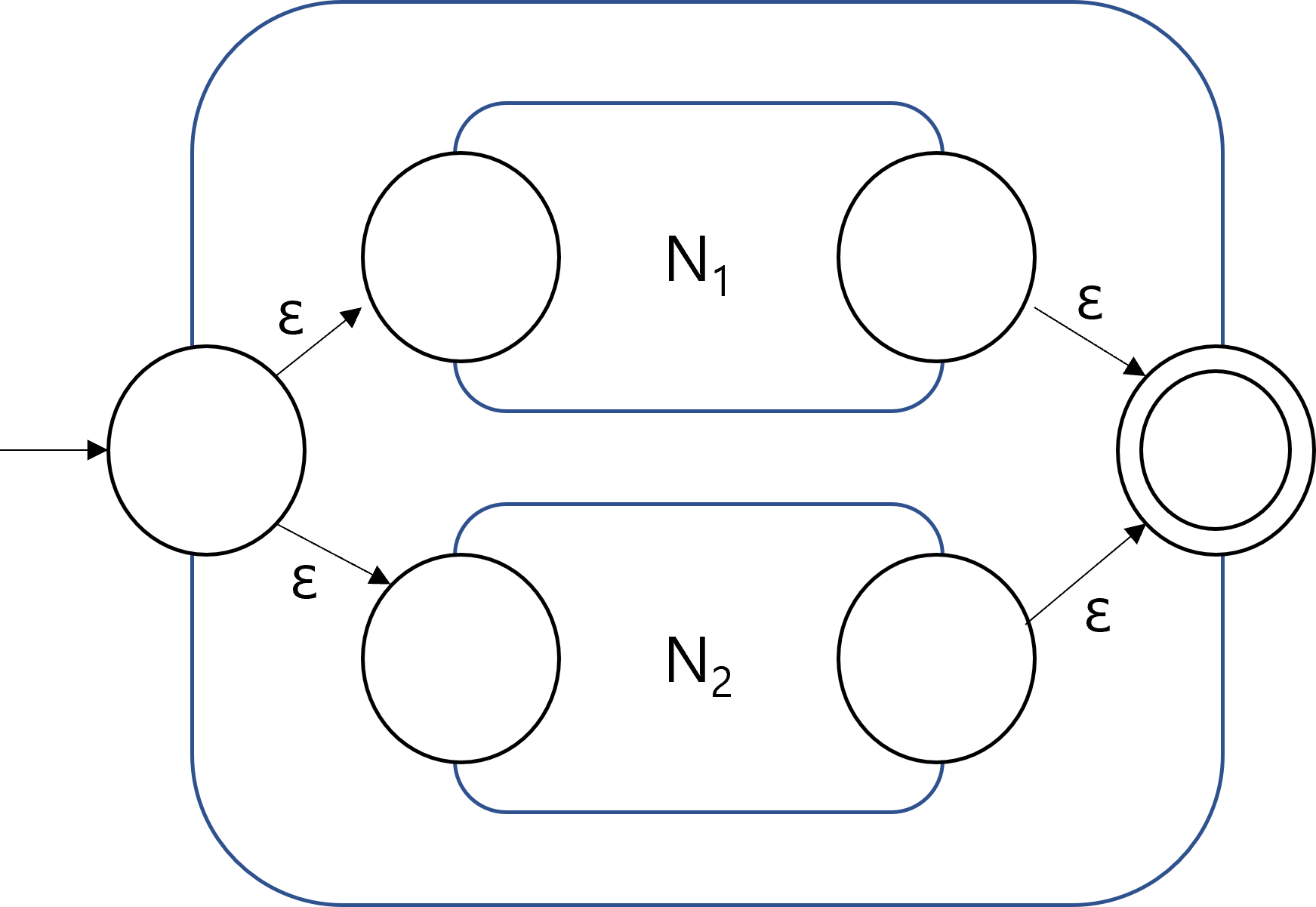
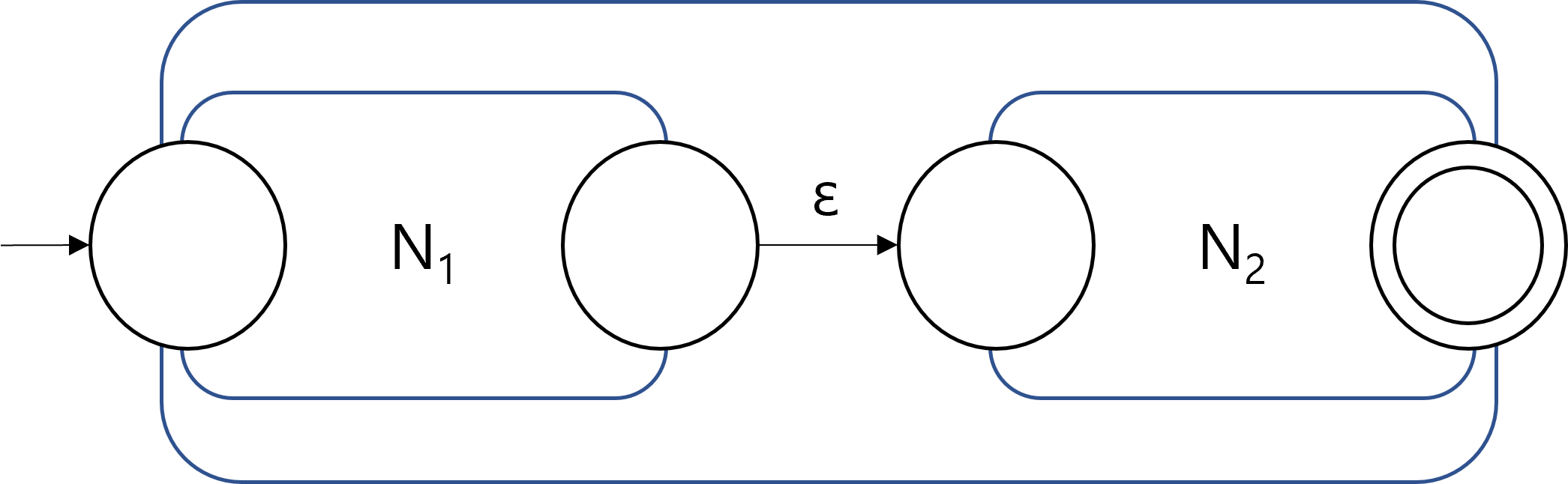
The closure properties of regular languages under union, concatenation, and Kleene Star can be proved using the transformed NFAs. The following figures show how the union, concatenation, Kleene star of regular languages can be constructed, given NFAs with a single accepting state.
| Union | Concatenation | Kleene Star |
|
|
|
Since the NFAs for the operations could be constructed, we conclude that the resulting languages are regular, and therefore the class of all regular languages is closed under the three operations. Note that the NFAs after applying the operations in the figures also have a single accepting state. Therefore, any combinations of unions, concatenations, and Kleene stars can be represented by recursively applying the construction method.
Terms and concepts
Power Set
The power set of a set $S$, often denoted as $2^S$, is a set of all subsets of $S$. For example, if $S=\{0, 1 \}$, then $2^S=\{\emptyset, \{0\}, \{1\}, \{0,1\} \}$.
$\epsilon$-Transition
An $\epsilon$-transition is a transition of an NFA that does not consume an input symbol. If there is an outgoing$\epsilon$-transition from the current state of an NFA, then the NFA can choose to either take the $\epsilon$-transition or not.
An $\epsilon$-reach of a state $q \in Q$ is a set of all states that can be reached from $q$ without reading in an input symbol. In the example NFA, the $\epsilon$-reach of the state $a$ is $\{a, b\}$. Note that $\epsilon$-reach of a state always contains the state itself.
Extended Transition Function
Describing transitions of an NFA on an input string requires applying transition function multiple times. The resulting expression would contain nested transition functions like $\delta(\delta(\delta(q,1),0),1)$, which can be wordy and confusing. Alternatively, we can define an extended transition function $\delta^{*}$ which defines transitions on an arbitrary string, as follows.
\[\delta^{*}(q,\epsilon):=\epsilon\text{reach}(q)\] \[\delta^{*} (q, ax) := \delta^{*} (\delta(q,a),x)\]Intuitively, the extended transition function is defined by recursively applying the transition function on the current state and the leftmost symbol of the remaining input string. The transition $\delta(\delta(\delta(q,1),0),1)$ introduced above can now be written as $\delta^{*}(q, 101)$. Note that defining the extended transition function does not change the behavior of the NFA at all. The extended transition function is more like a syntactic sugar derived from the original transition function.
Transformation
In the lab you went (will go) over language transformation. A language transformation is an operation on a language to transform it into a new language. An example is the language:
\[Flip(L) = \{\overline{w} \vert w \in L, \Sigma = \{0,1\)\}\]The transformation to turn a language \(L\) into a new language \(Flip(L)\) is pretty simple since all you’d need to do is take the DFA that describes \(L\) and change the \(0\)-transitions to \(1\)-transitions and vice-versa.
What we want to ask with language transformations is if these operations change the complexity class of the resulting language. We want to know if the input language(s) is(are) regular, is there a
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Sipser, Michael. Introduction to the Theory of Computation
- Chapter 1 - Regular Languages - 1.2 Non-determinism
- Sariel’s Lecture 4
- A video by Kevin Lim on language transformations

