Lecture 6 - Context-Free Languages and Push-down Automata

Context Free Language

• CFL is a higher level language when compared to Regular Language.
• CFL is a language that can be generated by some Context Free Grammar and is a set of all languages that can be accepted by a Push-down Automata.
  
  

Context Free Grammar

Formal Definition: Defined by 4 tuples G = (V, T, P, S)

• V = Finite set of Variables or Non-Terminal Symbols
• T = Finite set of Terminal Symbols
• S = Start symbol
• P = Finite set pf Production rules
  • Each production rule is represented as A→$\alpha$
  • Where $\alpha$ is a string in ${V \cup T}^*$ and A $\in$ V
    

Example: For generating a language with equal number of 0s and 1s of the form $0^{n}1^{n}$. We will have the G = ({S, A}, {0, 1}, {S→0A1, A→0A1 | $\varepsilon$}, S)

• S→0A1   (using S→0A1)
• →00A11   (using A→0A1)
• →000A111  (using A→0A1)
• →000111   (using A→$\varepsilon$)

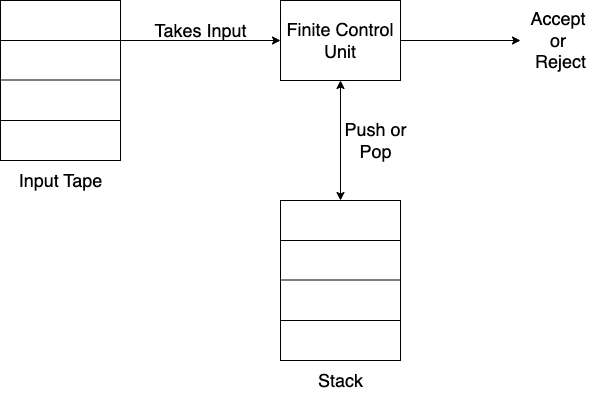
Push-down Automata

• A machine that generates Context Free Grammar
• It is more powerful than a Finite State Machine and also has more memory
• PDA = FSM + Stack
• Has 3 components:
  • Input
  • Finite Control Unit
  • Stack
    
    

Formal Definition: Defined by 6 tuples P = (Q, $\Sigma$, $\Gamma$, $\delta$, s, A)

• Q = finite set of states
• $\Sigma$ = finite set of input alphabets
• $\Gamma$ = finite set of stack alphabets
• s = start state
• A = set of accepting states
• $\delta$ = Transition Function

Transition Function $\delta$
$\delta$ = $Q\times\Sigma \cup {\varepsilon}\times\Gamma \cup {\varepsilon}$ → $P(Q \times (\Gamma\cup{\varepsilon}))$

• $\delta(q, a, X)$ → $(p, \gamma)$
• $q$ is a state in $Q$, $a$ is either an input in $\Sigma$ or $a=\varepsilon$, $X$ is a Stack symbol that ios part of $\Gamma$
• $p$ is a new state and $\gamma$ is string of stack symbols that replaces $X$ at the top of the stack
  • If $\gamma = \varepsilon$, then stack is popped
  • If $\gamma = X$, then stack is unchanged
  • If $\gamma = YZ$, then X is replaced by $Z$ and $Y$ is pushed into the stack

• $a$ = Input Symbol
• $b$ = Symbol on top of the stack which is pooped.
  • If $b=\varepsilon$, then stack is neither read or popped.
• $c$ = The Symbol that is pushed onto the stack
  • If $c=\varepsilon$, then nothing is pushed.

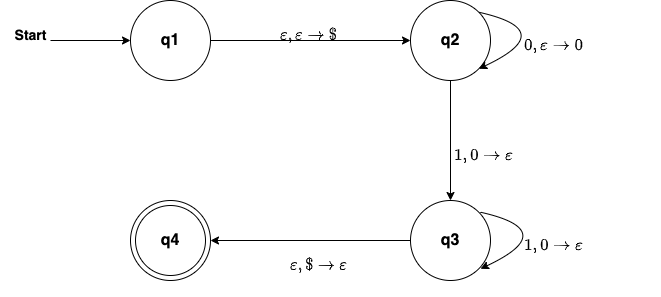
Example: Let’s construct a PDA that accepts the language $L = {0^n1^n | n\ge1}$

Closure Properties of CFL

Given two CFG $G_1 = (V_1, T, P_1, S_1)$ and $G_2 = (V_2, T, P_2, S_2)$ and assume that $V_1 \cap V_2 = \phi$. Let $L1$ and $L2$ be languages produced by $G1$ and $G2$ respectively.

• CFLs are closed under Union. $L_1 \cup L_2$ is a CFL.
• CFLs are closed under Concatenation. $L_1 . L_2$ is a CFL.
• CFLs are closed under Kleene star. If $L$ is a CFL $\implies L^*$ is a CFL.
• CFLs are not closed under Intersection
• CFLs are not closed under Complement

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Jeff’s Notes on Context Free language
  • Sipser, Michael. Introduction to the Theory of Computation
    • Chapter 2 - Context-Free Languages
• Sariel’s Lecture 7