Lecture 11 - Backtracking

Recursion

Recursion is a special case of reduction.

• A special case of reduction
• Reduce problem to a smaller instance of itself
• Self-reduction
• Problem instance of size n is reduced to one or more instances of size n 1 or less.
• For termination, problem instances of small size are solved by some other method as base cases.

Recursion in Algorithmic design

• Tail Recursion: problem reduced to a single recursive call after some work. Easy to convert algorithm into iterative or greedy algorithms. Examples: Interval scheduling, MST algorithms etc.
• Divide and Conquer: Problem reduced to multiple independent sub-problems that are solved separately. Conquer step puts together solution for bigger problem. Examples: Closest pair, median selection, quick sort.
• Backtracking: Refinement of brute force search. Build solution incrementally by invoking recursion to try all possibilities for the decision in each step.
• Dynamic Programming: problem reduced to multiple (typically) dependent or overlapping sub-problems. Use memorization to avoid re-computation of common solutions leading to iterative bottom-up algorithm

Backtracking

A backtracking algorithm tries to construct a solution to a computational problem incrementally, one small piece at a time. Whenever the algorithm needs to decide between multiple alternatives to the next component of the solution, it recursively evaluates every alternative and then chooses the best one.

State Tree

A state space tree is a tree constructed from all of the possible states of the problem as nodes, connected via state transitions from some initial state as root to some terminal state as a leaf.

Example 1 - The Queens problem

Problem -

1. How many queens can one place on the board?
2. Can one place 8 queens on the board?

Process:

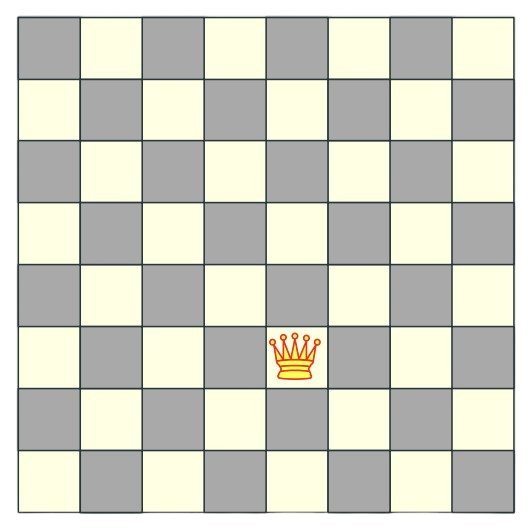
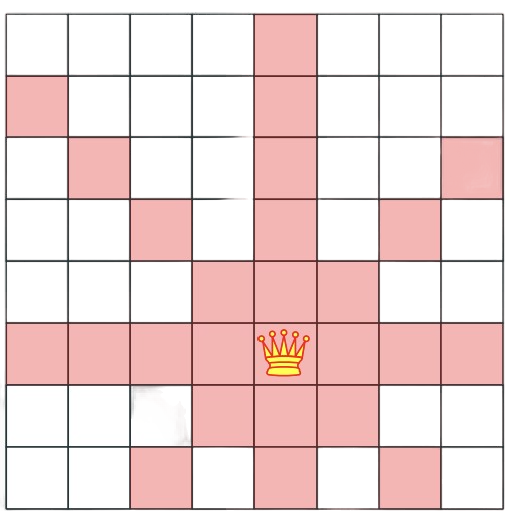
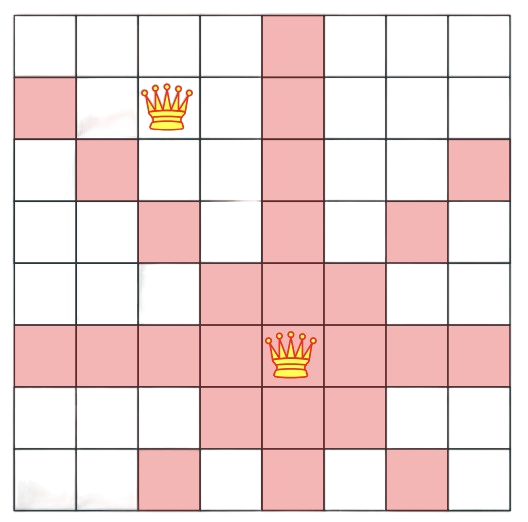
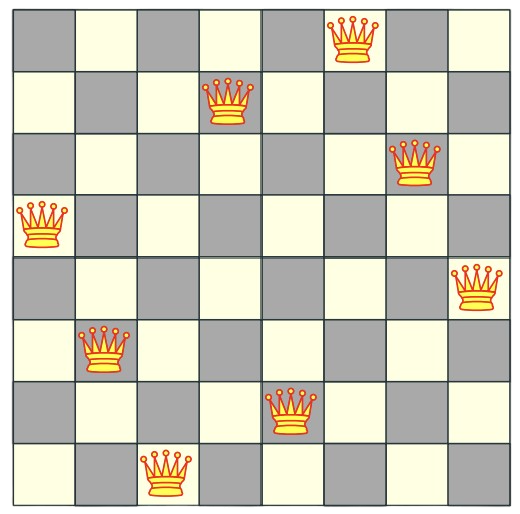
Initial board with Queen 1 placement.	All the possible places that the current queen can go to.	Queen 2 placement.	Final 8-Queen problem solved in 1850 (published in 1848)

Problem :

• How to solve problem for general n?

Intuition:

• Queens can’t be on the same row, column or diagonal
• Can have n queens max.

Search tree for 5 queens:

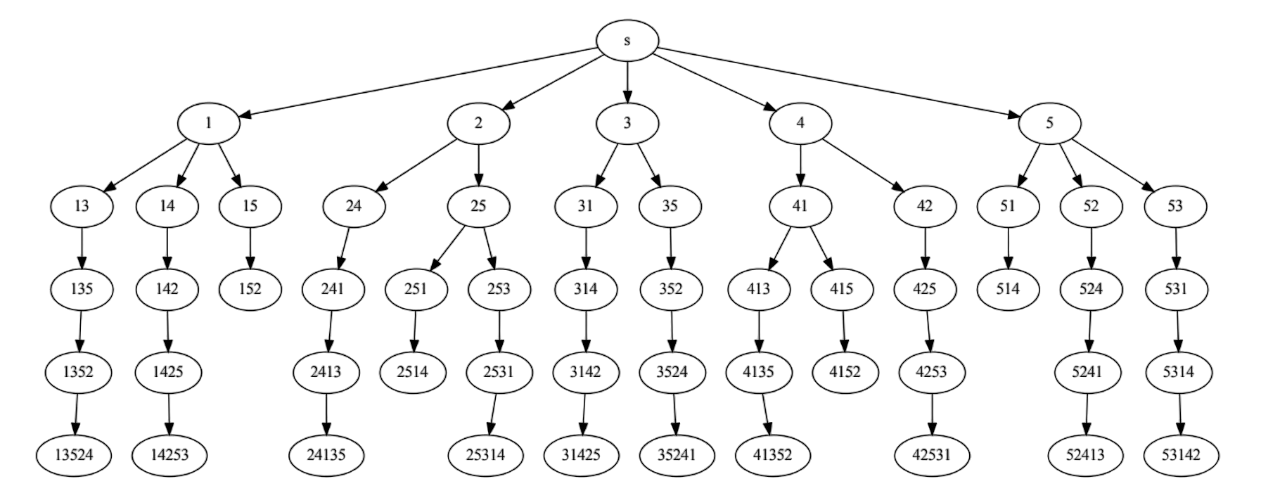
Each node in the state tree represents a board state. For eg. node 135 represents a board where the queens placed on column 1,3 and 5. The leaf nodes represent the final state of the board where either 5 queens are placed or it cannot proceed further.

Hence, we recursively search over an implicit tree, where we “backtrack” if certain possibilities do not work.

Longest Increasing Subsequence (LIS)

Definitions:

• Sequence: an ordered list $a_1$, $a_{2}$,…, $a_{n}$. Length of a sequence is number of elements in the list.
• Subsequence: $a_{i1}$ ,…, $a_{ik}$ is a subsequence of $a_{1}$,…, $a_{n}$ if 1 $\le$ $i_{1}$ < $i_{2}$ <…< $i_{k}$ $\le$ n.
• Increasing sequence: A sequence is increasing if $a_{1}$ < $a_{2}$ <…< $a_{n}$. It is non-decreasing if $a_{1}$ $\le$ $a_{2}$ $\le$ … $\le$ $a_{n}$. Similarly decreasing and non-increasing.

Problem:

• Input: A sequence of numbers $a_{1}$ , $a_{2}$,…, $a_{n}$
• Goal: Find an increasing subsequence $a_{i1}$ , $a_{i2}$ ,…, $a_{ik}$ of maximum length

1. Naive solution:
   

   algLISNaive(A[1..n]):
     max = 0
     for each subsequence B of A do
      if B is increasing and |B| > max then
        max = |B|
     Output max
   

   Running time: O(n$2^n$) for $2^n$ subsequences of a sequence of length n and O(n) time to check if a given sequence is increasing.

2. Recursive solution for LIS(A[1..n]):
   • Case 1: Does not contain A[n] in which case LIS(A[1..n]) = LIS(A[1..(n − 1)])
   • Case 2: Contains A[n] in which case LIS(A[1..n]) is not so clear.
   • Note: For second case we want to find a subsequence in A[1..(n − 1)] that is restricted to numbers less than A[n]. This suggests that a more general problem is LIS_smaller(A[1..n], x) which gives the longest increasing subsequence in A where each number in the sequence is less than x.

LIS_smaller(A[1..n], x):
  if (n = 0) then return 0
  m = LIS_smaller(A[1..(n − 1)], x)
  if (A[n] < x) then
    m = max(m, 1 + LIS_smaller(A[1..(n − 1)], A[n]))
  Output m

LIS(A[1..n]):
  return LIS_smaller(A[1..n], ∞)

Running time: O($2^n$)

General pattern

Backtracking algorithms are commonly used to make a sequence of decisions, with the goal of building a recursively defined structure satisfying certain constraints. Often (but not always) this goal structure is itself a sequence. For example:

• In the n-queens problem, the goal is a sequence of queen positions, one in each row, such that no two queens attack each other. For each row, the algorithm decides where to place the queen.
• In the LIS problem, the goal is a sequence of input elements that have an increasing order of value. For each input element, the algorithm decides whether to include it in the output sequence or not.

Relevent LeetCode Practice (by Tristan Yang)

1. LeetCode 51 — N-Queens (Hard)
   • Relevance: Exactly the slide’s example of backtracking: search tree DFS over rows, with pruning on columns and diagonals. Mirrors the typical generate_permutations + isValid approach for the N-Queens solution.
   • ECE 374 Process: Place queens row by row; maintain column, diag1, diag2 occupancy (using boolean arrays or bitmasks) to prune invalid moves. Use recursion to explore valid placements and backtrack upon conflicts. Analyze the exponential state-space and how pruning significantly reduces it.
   • Resource: NeetCode video on N-Queens (bitmask optimization approach).
   • Takeaway: Backtracking = DFS over the state space with constraints to prune branches early.
2. LeetCode 36 — Valid Sudoku (Medium)
   • Relevance: A constraint-checking problem; illustrates the “isValid” predicate central to backtracking, though here we mostly validate a full board rather than generate. We ensure each row, column, and 3×3 box meets constraints using sets or bitmasks.
   • ECE 374 Process: You can approach this as a backtracking search: precompute row/col/box usage masks; choose the next empty cell (optionally using MRV heuristic for fewest possible values), try a digit, update masks, recurse, and backtrack if a contradiction arises. (Alternatively, just validate an already-filled board by checking constraints, without full search.)
   • Resource: Errichto’s Sudoku backtracking video.
   • Takeaway: Efficient constraint checking (e.g. via bitmasks) enables pruning and is key to backtracking solutions.
3. LeetCode 300 — Longest Increasing Subsequence (Medium)
   • Relevance: Demonstrates turning an exponential brute force into a polynomial solution by memoization. Naively, LIS via brute-force subsequence generation is $O(2^n)$ (exponential). A smarter recursive approach that builds LIS ending at each element is still $O(2^n)$ without memoization. With memoization or dynamic programming, it becomes $O(n^2)$ (and with a greedy+binary-search optimization, $O(n \log n)$).
   • ECE 374 Process: Define the subproblem: $dp[i] = \max{1 + dp[j] : j < i, a_j < a_i}$ with base case $dp[i] = 1$. Memoize the recursive solution or fill an array iteratively. Optionally, discuss the patience sorting method for $O(n \log n)$.
   • Resource: NeetCode video on LIS (DP and patience sorting).
   • Takeaway: Memoization (or DP) can collapse an exponential recursion into a polynomial-time solution.

Supplemental Problems

• LeetCode 22 — Generate Parentheses
  Classic backtracking with a validity constraint (cannot add more ) than ( at any point). Explores a $2^n$-size state tree with pruning.

• LeetCode 78 — Subsets
  Pure backtracking (include/exclude each element), generating $2^n$ subset solutions, illustrating the power set exploration like the naive LIS approach.

• LeetCode 90 — Subsets II
  Backtracking with duplicate-handling: sort the input and skip consecutive duplicates to avoid repeat subsets.

• LeetCode 46 — Permutations
  Backtracking by building permutations position by position (tree of factorial size), just like the slide’s permutation generator example.

• LeetCode 47 — Permutations II
  Adds duplicate pruning on top of permutations (e.g. skip over used duplicate numbers) reinforcing the use of an isValid-style check.

• LeetCode 77 — Combinations
  Backtracking to choose k out of n (depth-first generation), with an early stopping optimization (stop exploring when not enough elements are left to reach k).

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Chapter 3 - Backtracking
  • Skiena, Steven. The Algorithms Design Manual
    • Chapter 9.1 - Backtracking
    • Chapter 9.2 - Examples of sBacktracking
• Sariel’s Lecture 12