Lecture 15 - Directed graphs, DFS, DAGs, TopSort

Date Pre-lecture slides Post-lecture scribbles Async video Lecture recording
October 21 2025 Lecture 15 - Directed graphs, DFS, DAGs, TopSort Lecture 15 - Directed graphs, DFS, DAGs, TopSort Lecture 15 - Directed graphs, DFS, DAGs, TopSort Lecture 15 - Directed graphs, DFS, DAGs, TopSort
 

Notes

Directed Acyclic Graph

Definition

A directed graph G is a directed acyclic graph (DAG) if there is no directed cycle in G.

Concatenation

Properties

Topological Ordering/Sorting

Definition

A topological ordering/topological sorting of G = (V, E) is an ordering $<$ on V such that if $(u → v) \in E $ then $u < v$ .

Informal Definition : One can order the vertices of the graph along a line (say the x-axis) such that all edges are from left to right.

Concatenation

Depth First Search

DFS with pre-post numbering in directed graphs

The Pre-visit number indicates when the node enters the DFS recursion stack, and the Post-visit number indicates when the node exits the DFS recursion stack. Pre and Post numbers can be used to determine whether a particular node is in the sub-tree of another node.

DFS(G)
    Mark all nodes u as unvisited
    T is set to ∅
    time = 0
    while there is an unvisited node u do
        DFS(u)
    Output T

DFS(u)
    Mark u as visited
    pre(u) = ++time
    for each edge (u, v) in Out(u) do
        if v is not visited
            add edge (u, v) to T
            DFS(v)
    post(u) = ++time
Properties
Example

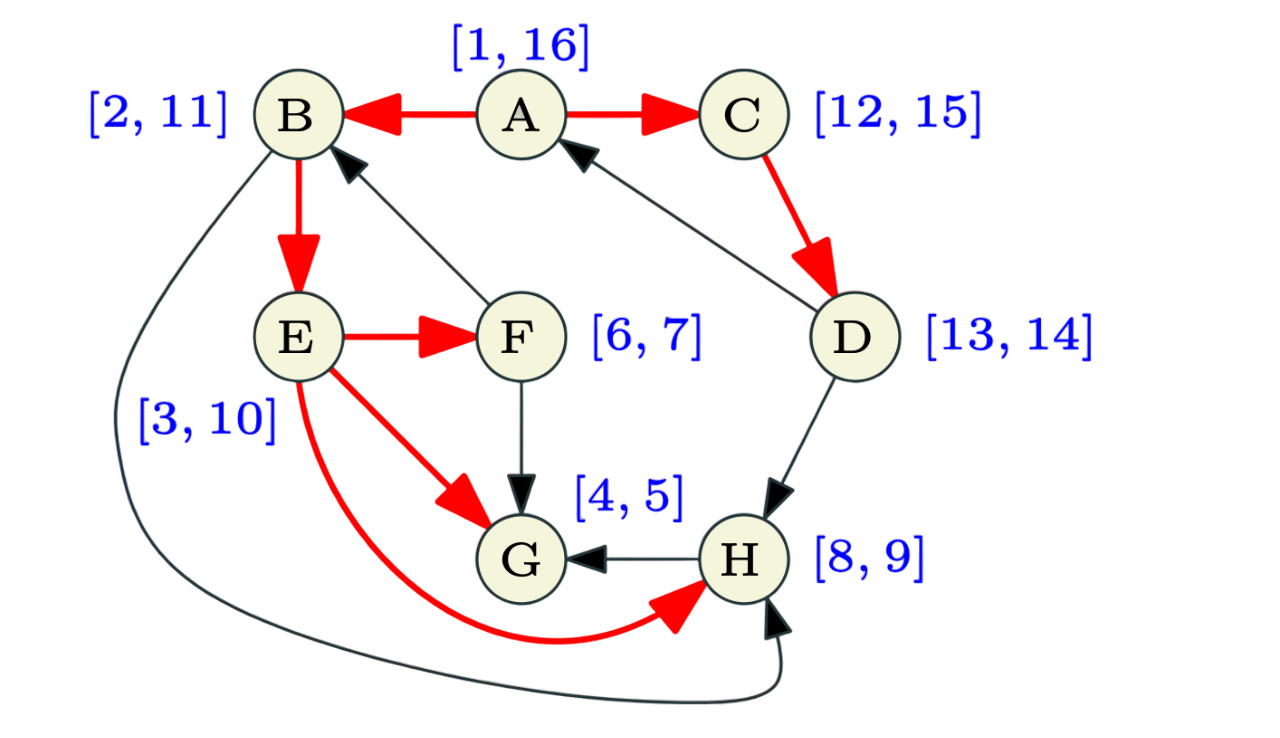
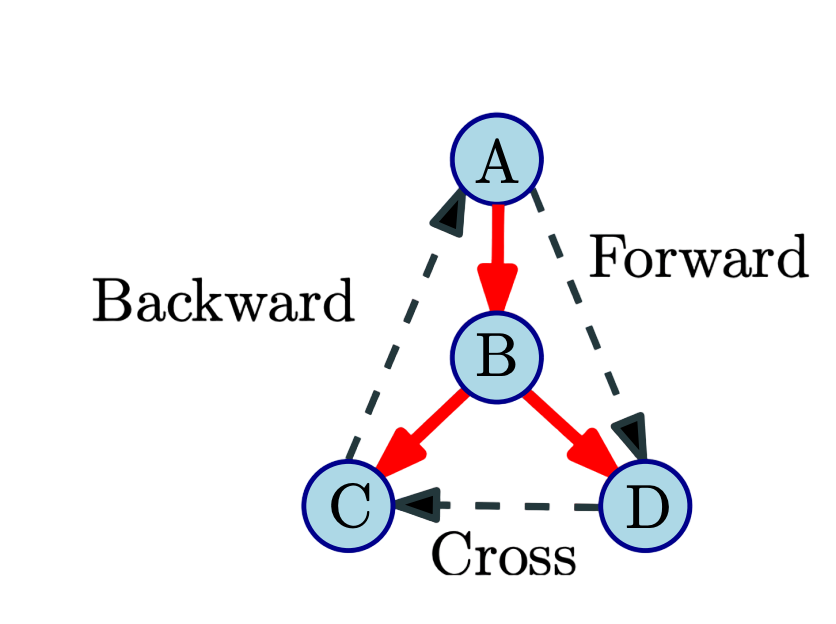
Concatenation

Edges of G can be classified with respect to the DFS tree T as:

Concatenation

Cycle detection in directed graph using topological sorting

Given a graph G, if it is a Directed Acyclic graph then compute a topological sort. If it failes, then output the cycle C.

The algorithm will be as follows:

The above algorithm runs in $O(n + m)$ time.

Graph of strong connected components

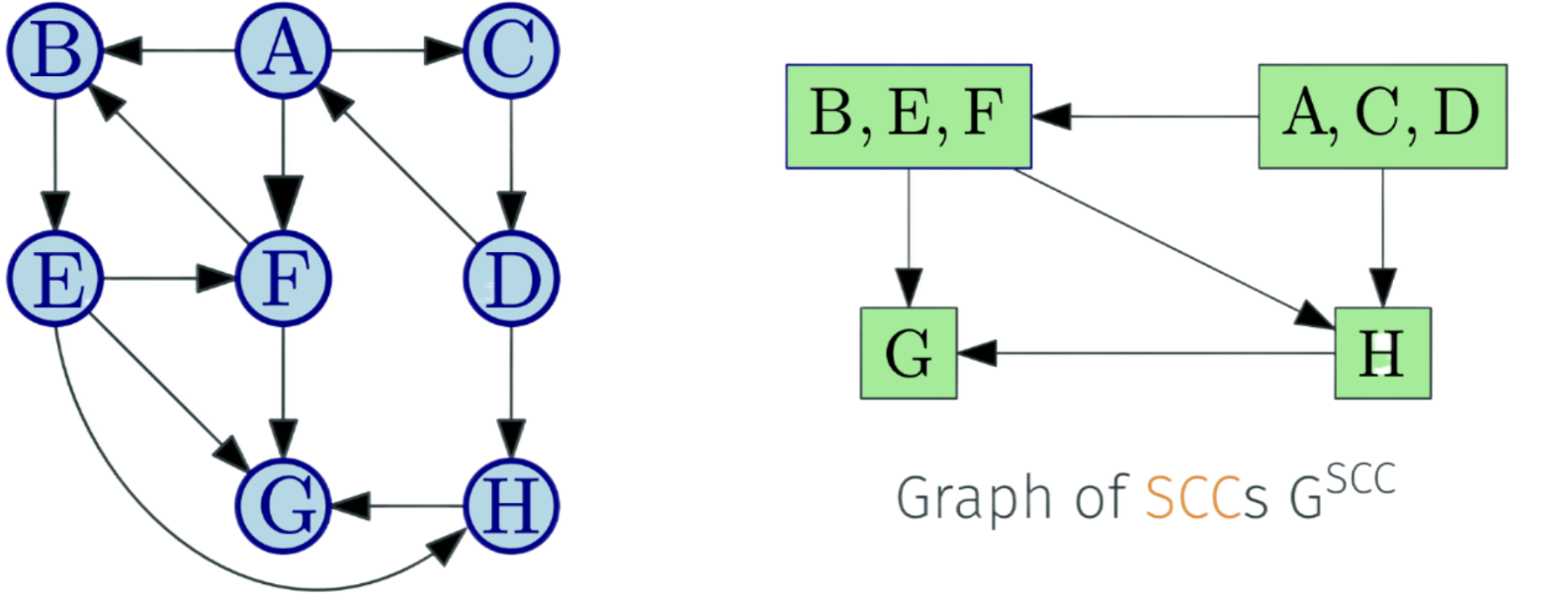
Concatenation

Let $S_1, S_2, . . . S_k$ be the strong connected components (i.e.,SCCs) of G. The graph of SCCs is $G^{SCC}$. It is created by collapsing every strong connected component to a single vertex.

For a directed graph G, its meta-graph $G^{SCC}$ is a DAG.

The straightforward algorithm(discussed in Lecture 15) to find all SCCs of a given directed graph has a running time of $O(n(n + m))$.

The Linear time Algorithm for SCCs will be as follows:

If v is the vertex with maximum post numbering in $DFS(G^{rev})$. Then v is in a SCC S, such that S is a sink of $G^{SCC}$. So, we can find a vertex in a sink SCC of $G^{SCC}$ for the linear time algorithm. Let us assume $G1=G^{rev}$.

do DFS(G1) and output vertices in decreasing post order.
Mark all nodes as unvisited
for each u in the computed order do
    if u is not visited then
        DFS(u)
        Let S1 be the nodes reached by u
        Output S1 as a strong connected component
        Remove S1 from G

The above algorithm runs in time $O(m + n)$ and correctly outputs all the SCCs of G.

Relevent LeetCode Practice (by Tristan Yang)

  1. LeetCode 210 — Course Schedule II (Medium)
    • Relevance: Requires producing an actual topological order of a directed acyclic graph (or detecting a cycle if one exists).
    • ECE 374 Process: Build the directed graph from course prerequisites. Then either: use Kahn’s algorithm (maintain an in-degree=0 queue and remove nodes one-by-one) or use DFS with 3-colors (marking nodes white/gray/black) and output nodes in decreasing post-order (which yields a topo sort). Runs in $O(n+m)$.
    • Resource: CP-Algorithms notes on Topological Sorting (both Kahn’s and DFS methods).
    • Takeaway: A graph is a DAG if and only if it has a topological order. In practice, using DFS post-order or Kahn’s BFS both produce a valid topo sort for DAGs.
  2. LeetCode 802 — Find Eventual Safe States (Medium)
    • Relevance: Identifies nodes that are not part of any cycle (i.e. eventually reach a terminal node). This is essentially finding vertices in a directed graph that belong to “acyclic” portions, using an approach akin to reasoning on the SCC condensation graph.
    • ECE 374 Process: Build the reverse graph (reverse all edges). Start with all nodes that have no outgoing edges in the original graph (these are terminal “safe” nodes). Perform a Kahn-like process: put all such sinks in a queue and remove them, decrementing the out-degree of their predecessors (in the original graph). Any predecessor that loses all outgoing edges becomes safe and is added to the queue. Nodes never marked safe are part of cycles.
    • Resource: Descriptions of the reverse-graph + Kahn’s algorithm trick for detecting cycle-free nodes.
    • Takeaway: Many queries about “eventually safe” (cycle-free) nodes reduce to iteratively peeling off sink nodes — conceptually working on the DAG of strongly connected components.
  3. LeetCode 269 — Alien Dictionary (Hard)
    • Relevance: A real-world application of topological sorting where nodes are characters and edges are precedence constraints derived from dictionary order. It deals with multiple valid orders and detecting inconsistencies (cycles).
    • ECE 374 Process: Read the list of words. Compare each adjacent pair of words to find the first differing character, and create a directed edge from that char of the first word to that of the second word. (If a word is a prefix of a later word, that’s invalid ordering.) Then perform a topological sort on the graph of letters. If you detect a cycle or if the result doesn’t include all letters that appeared, the dictionary order is invalid.
    • Resource: Detailed LeetCode editorials (for correctly building the graph and handling edge cases).
    • Takeaway: Modeling is critical: turn the problem’s implicit constraints into a directed graph. Then apply topo-sort to derive an order or find a contradiction (cycle).

Supplemental Problems

Additional Resources

Contributors

Sindhu Vydana
Sindhu Vydana

Site created by Nickvash Kani using the backend from the Mathematical Language Processing Group website.
Electrical and Computer Engineering Department at the University of Illinois at Urbana-Champaign