SAT
Definition:
For a set of boolean variables $x_1,x_2,…,x_n$
- A literal is either $x_i$ or $\neg x_i$
- A clause is a disjunction of literals
(i.e. $x_3 \lor \neg x_7 \lor x_8$)
- Conjunctive normal form (CNF) is a conjunction of causes
(i.e. $(x_1 \lor x_4) \land (x_3 \lor \neg x_7 \lor x_8) \land x_5$)
- 3CNF is a CNF formula where each clause has exactly 3 literals
Problem: SAT
For a given CNF (3CNF for 3SAT) formula $\phi$, is there a truth assignment of the variables such that $\phi$ evaluates to true?
Example:
- $(x_1 \lor x_4) \land (x_3 \lor \neg x_7 \lor x_8) \land x_5$ evaluates to true when every variable is set to true.
- $(x_1 \lor x_4) \land x_5 \land \neg x_5$ cannot evaluate to true because either $x_5$ or $\neg x_5$ will be false.
Reducing SAT to 3SAT:
To reduce from an instance of SAT to an instance of 3SAT all clauses must be made to have exactly 3 literals. To do this dummy variables are introduced such that the original formula is satisfiable if and only if the formula with the dummy variables is satisfiable. Short clauses are padded with dummy variables to have 3 literals, long clauses are broken apart using dummy variables to get 3 literals. Proof in Prof. Har-Peled’s lectures
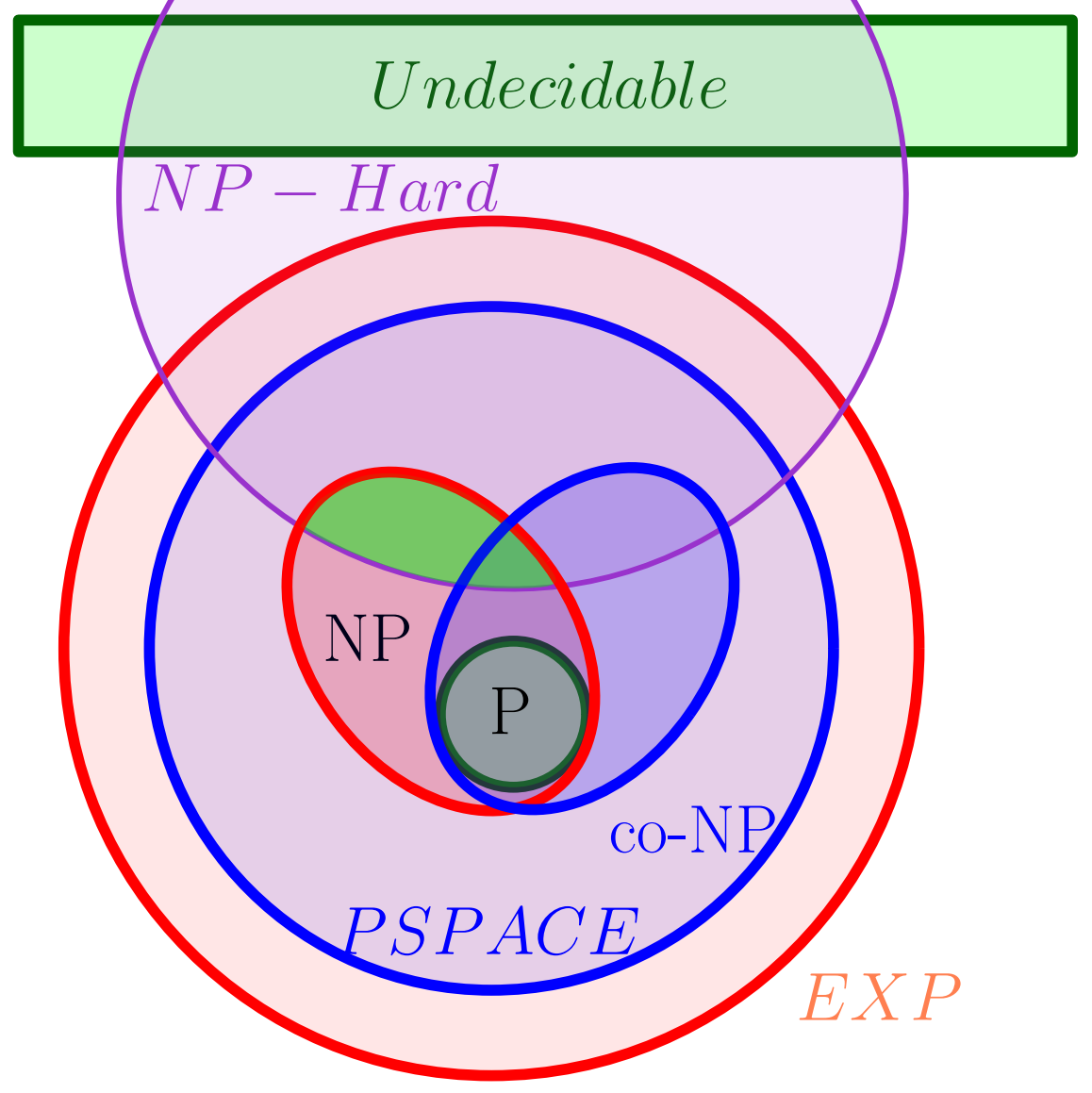
Complexity Classes
- P: the set of decision problems that have polynomial time algorithms.
- NP: the set of decision problems that have polynomial time non-deterministic algorithms. Every NP problem has an exponential time deterministic algorithm.
Problems with no known P solution:
- Independent Set
- Vertex Cover
- Set Cover
- SAT
Certifier:
An algorithm $C(\cdot,\cdot)$ is a certifier for a problem $X$ if
- For every $s\in X$ there is some string $t$ such that $C(s,t)$ = “yes”
- If $s\not\in X$ then $C(s,t)$ = “no” for every $t$
The string $s$ is the problem instance (i.e. a particular graph for vertex cover problem, a CNF formula for SAT problem). The string $t$ is called the certificate or proof for $s$.
Efficient Certifier:
A certifier $C$ is an efficient certifier for problem $X$ if there is a polynomial $p(\cdot)$ such that
-
For every $s \in X$ there is some string $t$ such that $C(s,t)$ = yes and $ t \leq p( s )$ - If $s\not\in X$ then $C(s,t)$ = “no” for every $t$
- $C(\cdot,\cdot)$ runs in polynomial time
Example:
- Problem: Does $G = (V,E)$ have an independent set of size $\geq k$?
- Certificate: Set $S \subset V$
-
Certifier: Check $ S \geq k$ and no pair of vertices in $S$ is connected by an edge ( $O(n^2)$ )
- Problem: Does CNF formula $\phi$ have a satisfying assignment?
- Certificate: Assignment $a$ 0/1 values to each variable.
- Certifier: Check each clause under $a$ and return “yes” if all clauses are true ( $O(n)$ )
Cook-Levin Theorem
NP-Hard:
A problem $X$ is NP-Hard if for any $Y \in$ NP, $Y \leq_P X$
NP-Complete:
A problem $X$ is NP-Complete if $X$ is both NP and NP-Hard
Lemma:
Suppose $X$ is NP-Complete. Then $X$ can be solved in polynomial time if and only if P=NP
Theorem (Cook-Levin):
SAT is NP-Complete
SAT $\leq_P X$ implies that every NP problem $Y\leq_P X$. $Y\leq_P$ SAT (Cook-Levin) and SAT $\leq_P X$ implies $Y\leq_P X$.
Example NP-Hard reductions in the lecture slides
- Independent Set (slides 34-38)
- Graph Coloring (slides 39-41)
- Hamiltonian Cycle (slide 42)
Reductions example
Your very own, Mr. Kevin Lim, did an animation of a classic 374 reduction:
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Sipser, Michael. Introduction to the Theory of Computation
- Chapter 7.4 - Polynomial time reducibility
- Skiena, Steven. The Algorithms Design Manual
- Chapter 11 - NP-completeness
- Sedgewick, Robert and Wayne, Kevin. Algorithms (Forth Edition)
- Chapter 6 - Context.Reductions
- Cormen, Thomas, et al. Algorithms (Forth Edition)
- Chapter 32 - NP-Completeness
- Jeff’s - Notes on NP-Hardness
- Sariel’s Lecture 22