Deterministic Finite Automata
Graphical Representation:
- DFAs are collections of states (vertices) with directed transitions (edges) that are labeled with symbols from an input set $\Sigma$
- Each state has exactly one outgoing transition for each symbol in $\Sigma$
- There is a unique state labeled the start state which is represented by an input arrow
- There is a unique set of states labeled the accepting states which are represented by double circles
Formal Representation: Defined by 5 tuples $M = (Q, \Sigma, s, A, \delta)$
- $Q$ is a finite set of states
- $\Sigma$ is a finite set inputs
- $s \in Q$ is the start state
- $A\subset Q$ are the accepting states
- $\delta: Q \times \Sigma \rightarrow Q$ are the state transitions
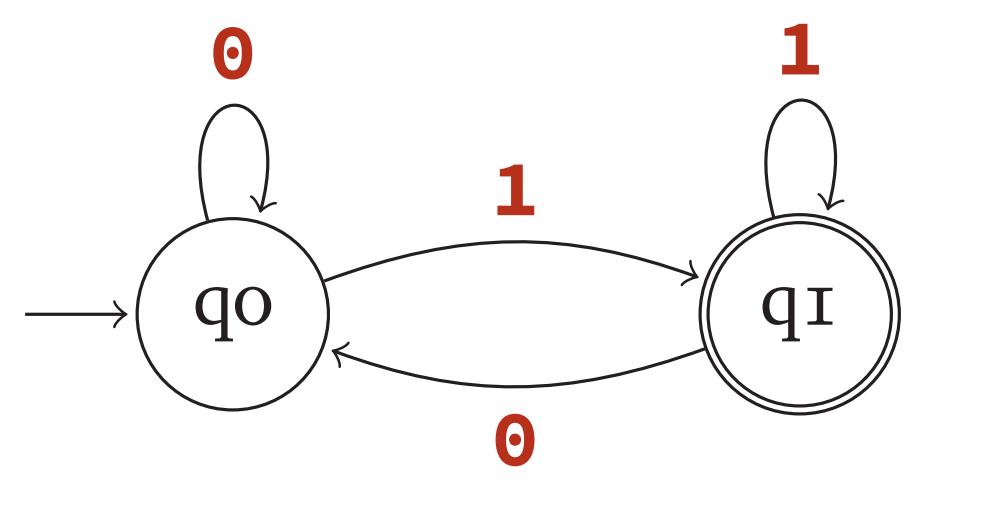
Example:
- $Q$ = { $q_0,q_1$ }
- $\Sigma$ = { $0,1$ }
- $s$ = $q_0$
- $A$ = { $q_1$ }
- $\delta(q_0,0) = q_0$, $\delta(q_1,1) = q_1$, $\delta(q_0,1) = q_1$, $\delta(q_1,0) = q_0$
Definitions:
- DFA M accepts a string w iff the unique walk begining at the start state and sequentially inputing the symbols in w ends on an accepts state.
- The language accepted (or recognized) by a DFA is the set of strings accepted by the DFA
Formal Definitions:
- A state transition with string input w is defined by $\delta^\ast(q,w) = \delta^\ast (\delta(q,a),x)$ where $w = ax$
- The language $L(M)$ accepted by a DFA $M = (Q, \Sigma, s, A, \delta)$ is defined as $L(M)$ = { $w \in \Sigma^\ast | \delta^\ast(s,w)\in A$ }
Theorems
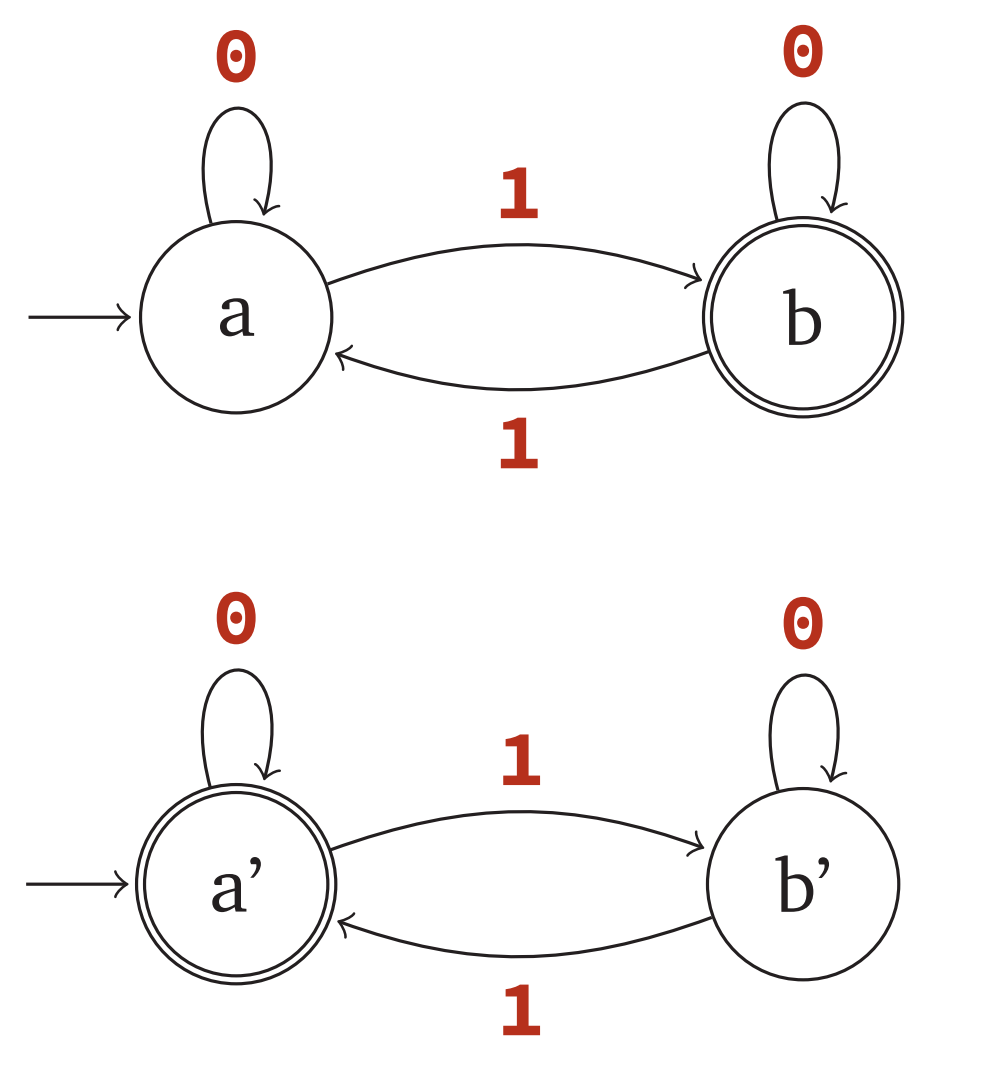
Languages accepted by DFAs are closed under compliment
If $L$ is accepted by $M_1 = (Q, \Sigma, s, A, \delta)$, then $\bar{L}$ is accepted by $M_2 = (Q, \Sigma, s, \bar{A}, \delta)$ where
- $\bar{A}$ = { $q\in Q | q \notin A$ }
Example:
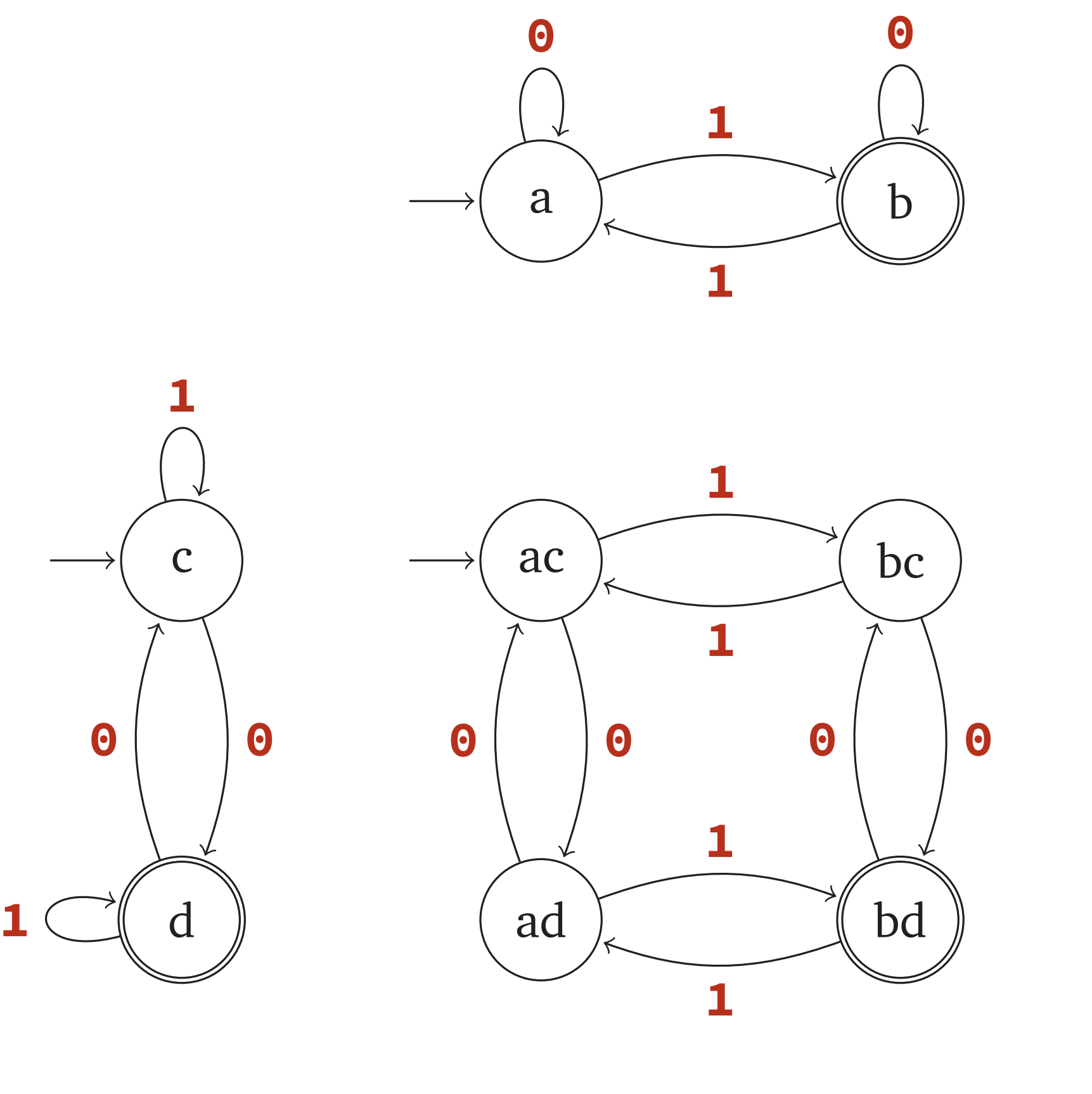
Languages accepted by DFAs are closed under intersection
If $L_1$ is accepted by $M_1 = (Q_1, \Sigma, s_1, A_1, \delta_1)$ and $L_2$ is accepted by $M_1 = (Q_1, \Sigma, s_2, A_2, \delta_2)$ then $L_1 \cap L_2$ is accepted by $M = (Q, \Sigma, s, A, \delta)$ where
- $Q$ = $Q_1 \times Q_2$
- $s$ = $(s_1,s_2)$
-
$A$ = { $(q,w)\in Q q \in A_1 \text{ and } w \in A_2$ } - $\delta((q,w),a) = (\delta_1(q,a),\delta_2(w,a))$
Example:
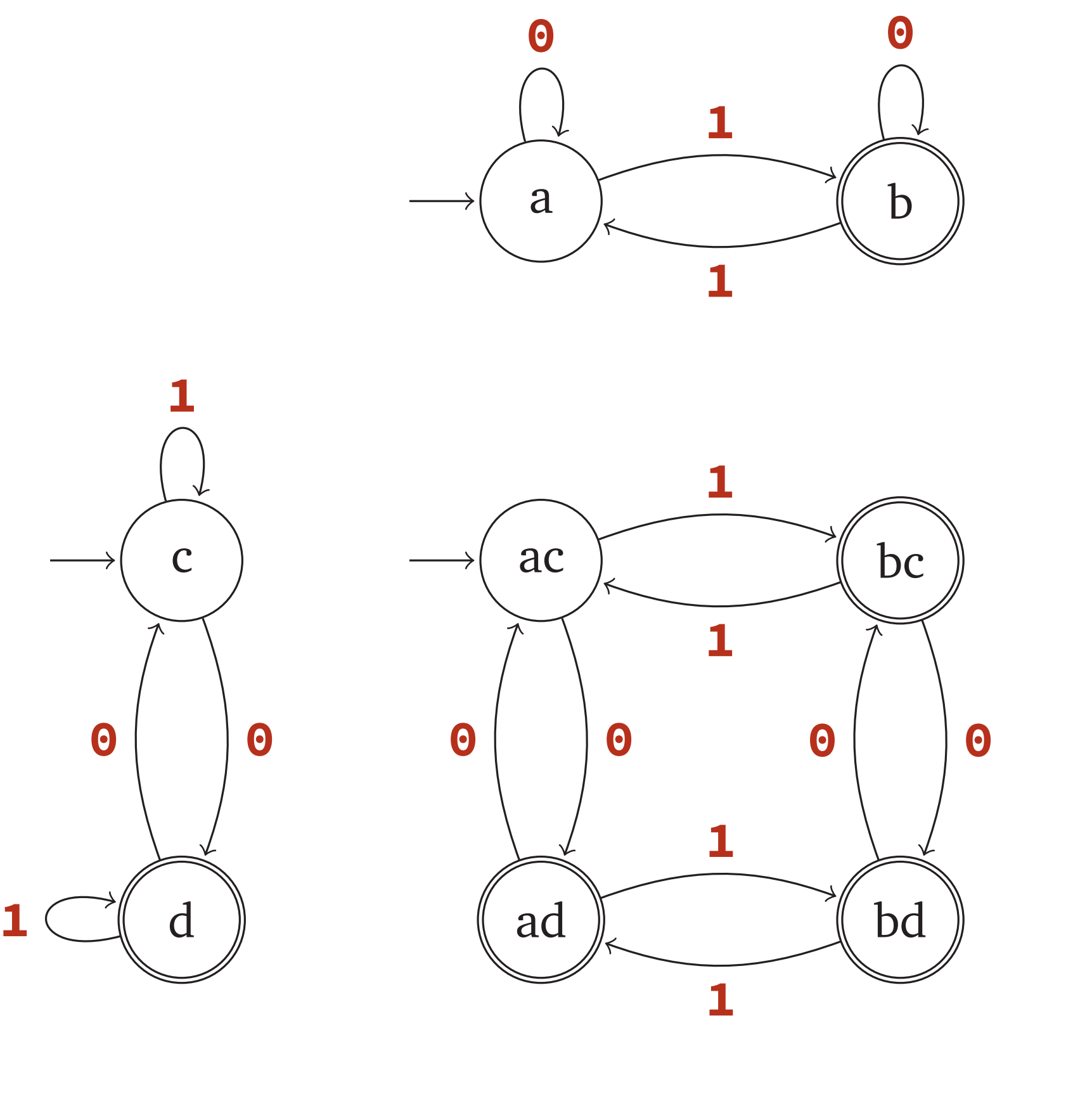
Languages accepted by DFAs are closed under union
If $L_1$ is accepted by $M_1 = (Q_1, \Sigma, s_1, A_1, \delta_1)$ and $L_2$ is accepted by $M_1 = (Q_1, \Sigma, s_2, A_2, \delta_2)$ then $L_1 \cap L_2$ is accepted by $M = (Q, \Sigma, s, A, \delta)$ where
- $Q$ = $Q_1 \times Q_2$
- $s$ = $(s_1,s_2)$
-
$A$ = { $(q,w)\in Q q \in A_1 \text{ or } w \in A_2$ } - $\delta((q,w),a) = (\delta_1(q,a),\delta_2(w,a))$
Example:
Constructing Regular Expressions from DFAs
In depth in Lecture 5
State Elimination: Slides 28-31 (55-60)
Algebraic Method: Slides 34-37 (64-68)
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Sipser, Michael. Introduction to the Theory of Computation
- Chapter 1 - Regular Languages - 1.1 Finite Automata
- Sariel’s Lecture 3