1. DFA → NFA
All DFAs can represent any languages that are represented by NFAs. All DFAs by definition are NFAs.
2. NFA → DFA
Consider any non-deterministic finite automata (NFA) N = $(Q, \Sigma, \delta, s, A)$ where :
• Q is a finite set whose elements are called states,
• $\Sigma$ is a finite set called the input alphabet,
• $\delta$ : Q × $\Sigma$ $\cup$ {$\epsilon$} → P(Q) is the transition function (here
P(Q) is the power set of Q),
• s ∈ Q is the start state,
• A ⊆ Q is the set of accepting/final states.
$\delta$(q, a) for a $\in$ $\Sigma$ $\cup$ {$\epsilon$} is a subset of Q — a set of states.
An equivalent DFA D = $(Q’, \Sigma, \delta’, s’, A’)$ can be constructed using the Subset State Construction such that:
• $Q’ = P(Q)$
• \(s' = \epsilon reach(s) = \delta^{*}(s,\epsilon)\)
• $A’ = { X \subseteq Q | X \cap A \neq \emptyset}$
• $\delta’(X, a) = \bigcup\limits_{q \in X} \delta^{*} (q,a) for each X \subseteq Q , a \in \Sigma$
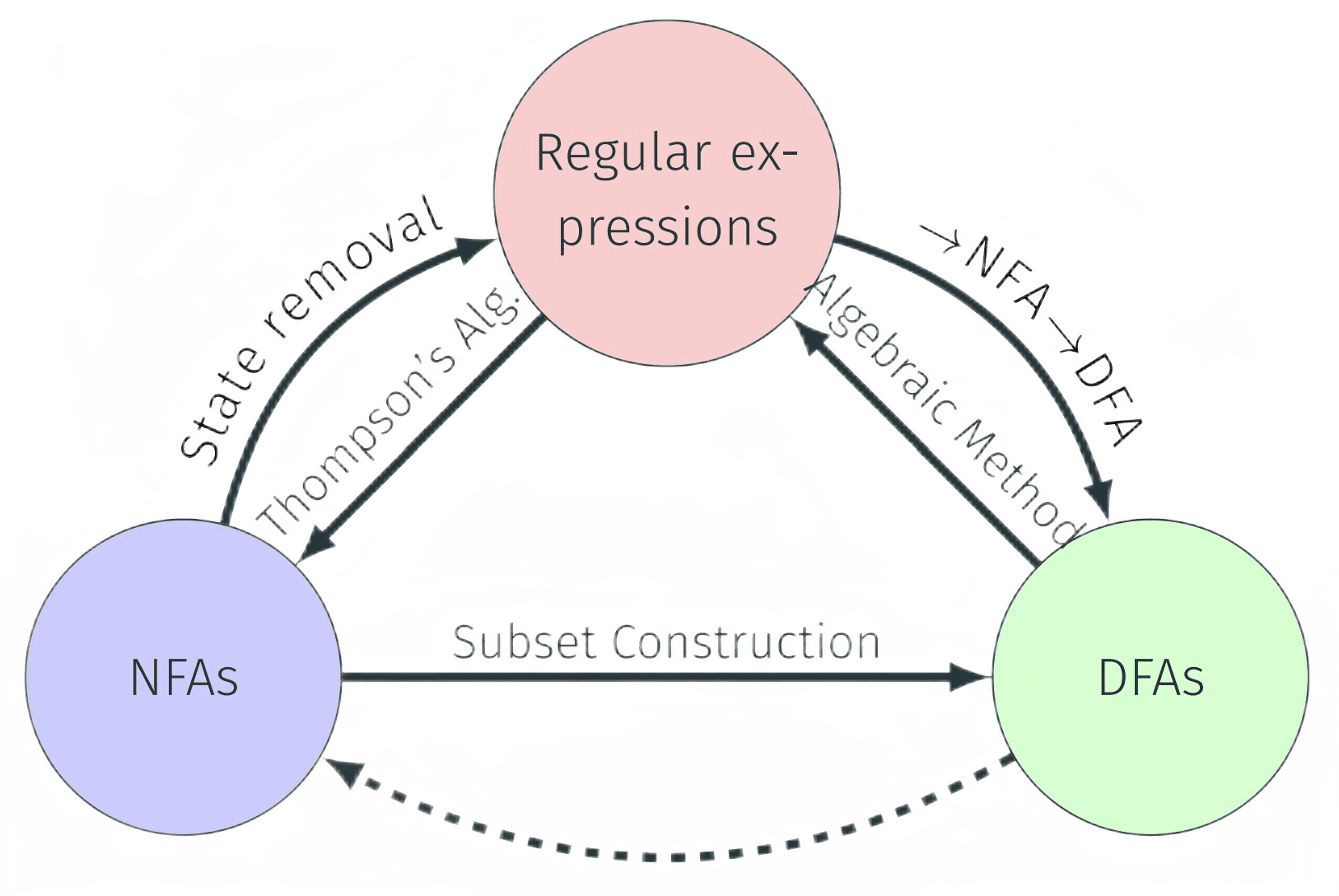
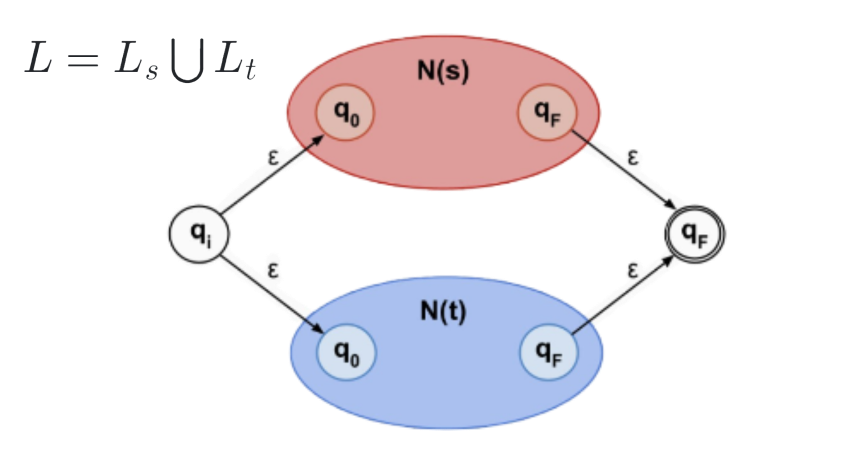
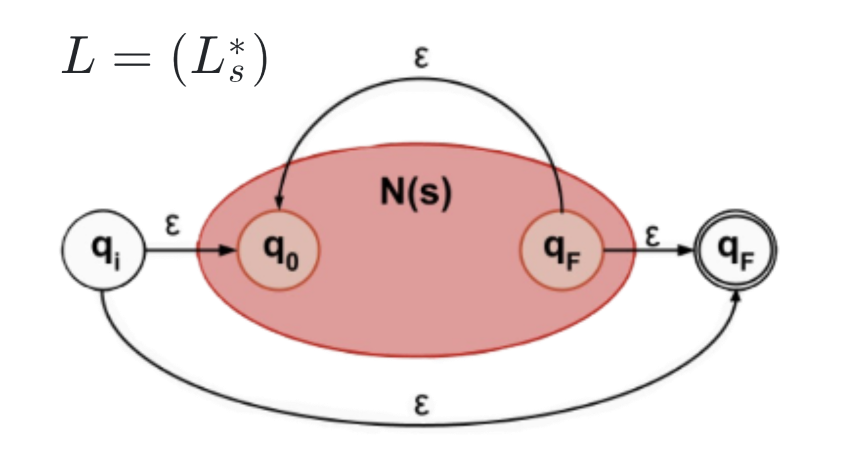
3. Regular Expressions → NFA
Any regular expression can be converted to an NFA using the Thompson’s Algorithm as follows:
|

|
|
Example: Construct a NFA for (101 + 010)

4. DFA → Regular Expressions
A Regular expression can be obtained from a DFA using two methods.
A. State Removal Method
If q1 = $\delta$(q0, x) and q2 = $\delta$(q1, y), then q2 = $\delta$(q1, y) = $\delta$($\delta$(q0, x), y) = $\delta$(q0, xy). This way, we can eliminate state q1.
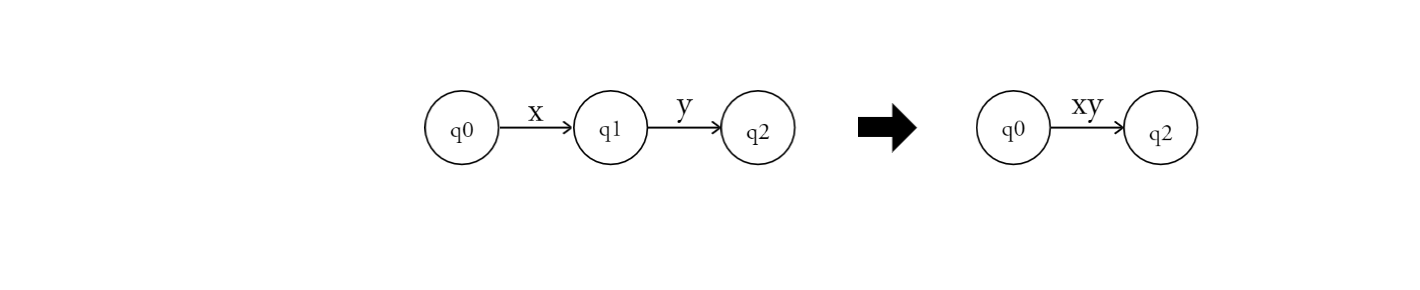
Example:
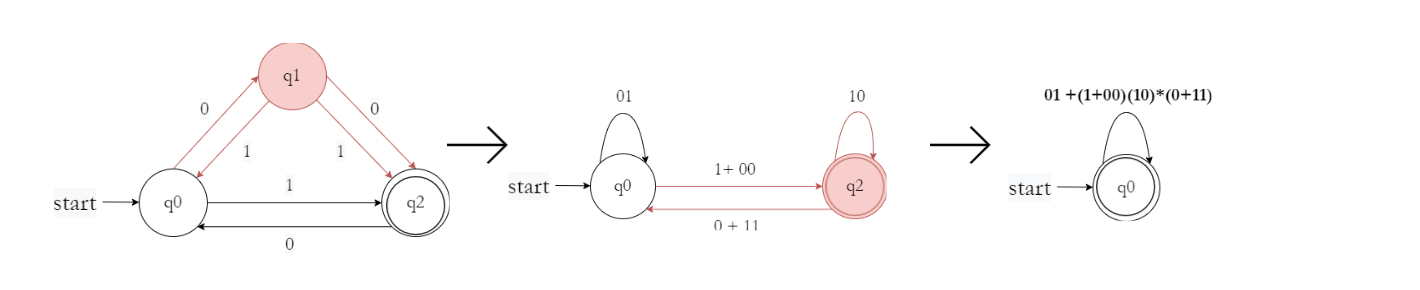
Therefore, the resulting regular expression for the given DFA is $(01 + (1 + 00)(10)^{∗}(0 + 11))^{∗}$
B. Algebraic Method
This method involves treating transition functions as algebraic expressions. That is, $q_1 = \delta(q_0, x)$ can be written as $q_1 = q_0x$ and the resulting expressions can be solved for the accepting state.
Example: Convert the following DFA to regular expression using Algebraic Method.
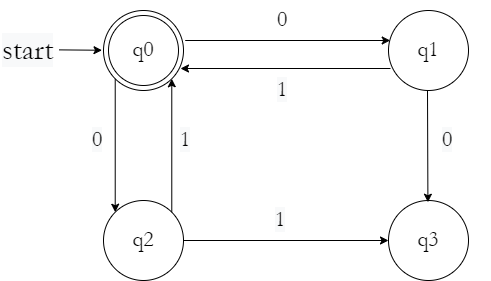
Writing down transitions as algebraic functions :
• $q_{0} = \epsilon + q_{1}1 + q_{2}0$
• $q_{1} = q_{0}0$
• $q_{2} = q_{0}1$
• $q_{3} = q_{1}0 + q_{2}1 + q_{3}(0 + 1)$
Now we simple solve the system of equations for $q_{0}$:
• $q_{0} = \epsilon + q_{1}1 + q_{2}0$
=> $q_{0} = \epsilon + q_{0}01 + q_{0}10$
=> $q_{0} = \epsilon + q_{0}(01 + 10)$
Make use of Theorem (Arden’s Theorem) that states $R = Q + RP = QP^{∗}$
=> $q_{0} = \epsilon(01 + 10)^{∗} = (01 + 10)^{∗}$
5. NFA → Regular Expressions
Any NFA can be converted to regular expressions using the same two methods as listed above :
• Algebraic Method - Treat transition functions as algebraic functions and solve for accepting state.
• State Removal Method - Normalize the NFA to have an isolated starting and ending state and then follow the same process as listed above.
Example:
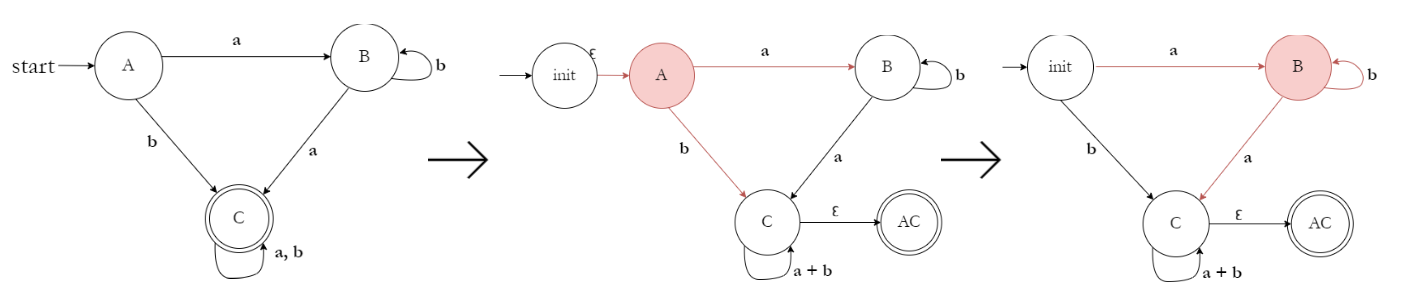
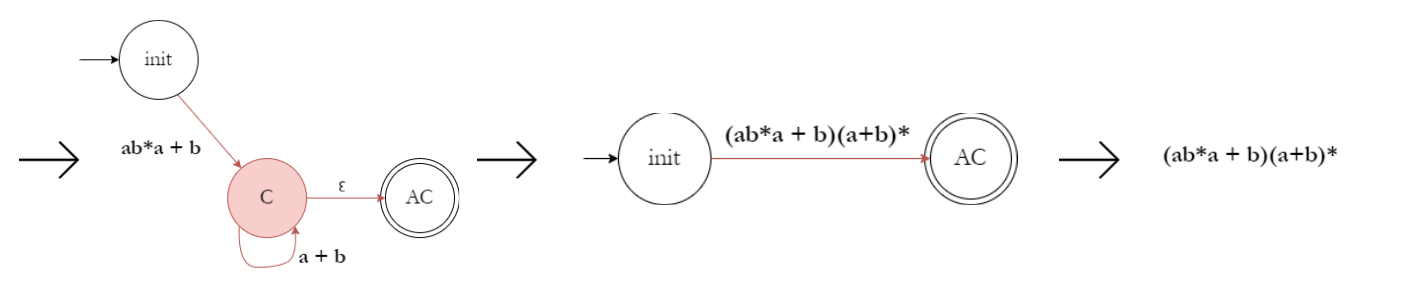
6. Regular Expressions → DFA
To convert Regular Expressions to DFA we can make use of the Brzozowski derivative, where ($u^{−1}$ S) of a set S of strings and a string u is the set of strings obtainable from a string in S by cutting of the prefix u.
Example: To construct language $R = (ab + c)^{*}$
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Sipser, Michael. *Introduction to the Theory of Computation
- Chapter 1 - Regular Languages
- Sariel’s Lecture 5
- Check out Mike Montano’s NFA-to-DFA subset construction tool to visualize how to convert a NFA to a DFA!
- Rust has a pretty robust RegEx library and a former 374-er spent some time investigating Rust’s procedural macros and how to convert a RegEx to a NFA. It’s a super interesting analysis requiring knowledge of grammars and programming paradigms. Check it out

