Lecture 5 (Abraham) - Non-regularity and fooling sets

Non-Regular Language

Definition

A Non-regular language is a type of formal language that cannot be defined by a regular expression or recognized by a finite automata. If a language contains strings where the necessary memory increases with the length of the string, it is probably not a regular language.

Example

A Simple and Canonical Non-regular Language:

L = { $0^{n} 1^{n}$ | $n \ge 0$}

This language cannot be considered regular, as recognizing it requires counting the number of zeros in the input, which cannot be done using a fixed amount of memory.

Methods for Proving Non-regularity

1) Pumping Lemma
2) Fooling sets(Distinguishing suffixes)
3) Closure properties

Fooling Sets

Before diving into the concept of fooling sets, let’s first understand the concept of distinguishable states and when two strings are considered distinguishable with respect to a language.

Distinguishable States

For a DFA M = (Q, $\Sigma$, $\delta$, s, A). Two states $p, q \in Q$ are distinguishable if there exists a string $w \in \Sigma^{*}$, such that

$\delta^* (p,w) \in A$ and $\delta^* (q,w) \not \in A$

or

$\delta^* (p,w) \not \in A$ and $\delta^* (q,w) \in A$

Example

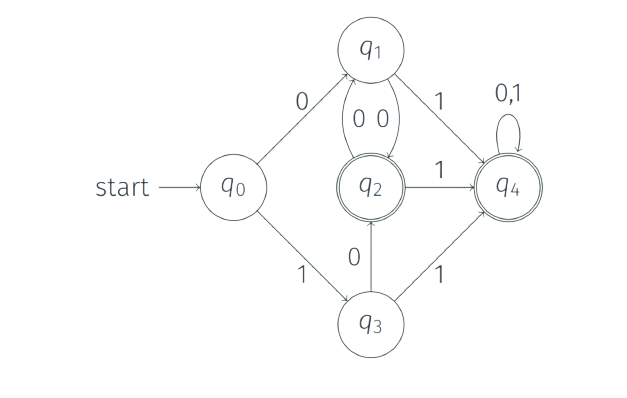
Let us take two states $q_{0}$ and $q_{1}$ from the above DFA. Let w=0,

$\delta(q_{0},0)=q_{1} \not \in A$

$\delta(q_{1},0)=q_{2} \in A$

Therefore, $q_{0}$ and $q_{1}$ are distinguishable states.

Distinguishable Prefixes

Two strings x and y are distinguishable for a Language L if there exists a suffix w such that exactly one of xw and yw belongs to L.

These distinguishable prefixes will result in distinguishable states when we construct a DFA or NFA.

Proof by figure

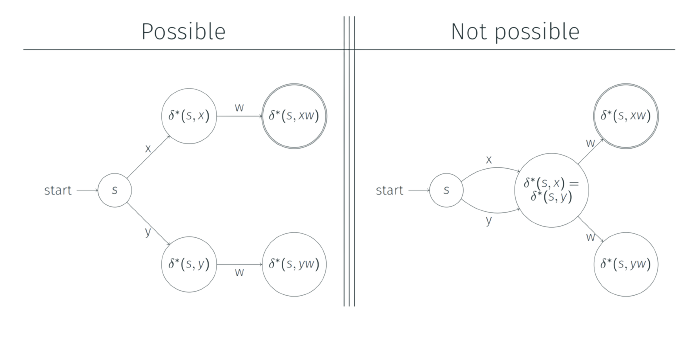
Here, x and y are distinguishable prefixes as they end up in distinguishable states which cannot be merged. xw and yw are distinguishable as $xw \in L$ and $yw \not \in L$.

Fooling Sets-Definition

For a language L over $\Sigma$ a set of strings F (could be infinite) is a fooling set or distinguishing set for L if every two distinct strings $x, y \in F$ are distinguishable.

If a Language L has an infinite fooling set F then L is not regular. If a language has an infinite fooling set, it will lead to an infinite number of distinguishable prefixes, requiring an infinite number of states to recognize the language. Since a Finite automata (DFA/NFA) cannot have an infinite number of states, it is not possible to construct a Finite automata for the language, making it a non-regular language.

The fooling set method is a proof by contradiction technique which involves the following steps:

1. Select a set of strings (x,y) as the prefixes of strings in the language.
2. Show that for a suffix z, either xz or yz belongs to the language L, making x and y distinguishable prefixes.
3. In the DFA representing language L, the states representing these prefixes must be distinct because they are distinguishable prefixes.
4. If there are an infinite number of distinguishable prefixes, then the DFA representing the language would have an infinite number of states.
5. Since this is not possible, a DFA cannot represent the language, thus the language is not regular.

Example

Prove language L = $\{0^{n} 1^{n} | n \ge 0 \}$ is not regular using fooling sets.

Solution

Let, F = $\{0^{i} | i \ge 0\}$ be the fooling set for the Language L.

Then, $x=0^{i},y=0^{j}$ for some non-negative integers i and j where $i \not = j$

Let, $z = 1^{i}$

Then, $xz = 0^{i}1^{i} \in L $

And $yz= 0^{j}1^{i} \not \in L$ as $i \not = j$

Thus, F is a fooling set for L. Because F is infinite, L cannot be regular.

Closure Properties

Using existing non-regular languages and regular languages we prove that some new language is non-regular. If we have to prove a Language L is non-regular. We combine L with known regular languages using regularity-preserving operations, to obtain a known non-regular language.

Consider, $L’ = L \cap (0^* 1^*)$

If L’ is a known non-regular language then it implies that L is non-regular. Why? Suppose L is regular. Then since $(0^* 1^*)$ is regular, and regular languages are closed under intersection, L’ also would be regular. But we know L’ is not regular, a contradiction. This means that L is also not regular.

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Jeff’s - Notes on finite-state automata
  • Sipser, Michael. Introduction to the Theory of Computation
    • Chapter 1 - Regular Languages - 1.4 Nonregular languages
• Sariel’s Lecture 6