Lecture 11 (Kani) - Backtracking

Recursion

Recursion is a special case of reduction.

• A special case of reduction
• Reduce problem to a smaller instance of itself
• Self-reduction
• Problem instance of size n is reduced to one or more instances of size n 1 or less.
• For termination, problem instances of small size are solved by some other method as base cases.

Recursion in Algorithmic design

• Tail Recursion: problem reduced to a single recursive call after some work. Easy to convert algorithm into iterative or greedy algorithms. Examples: Interval scheduling, MST algorithms etc.
• Divide and Conquer: Problem reduced to multiple independent sub-problems that are solved separately. Conquer step puts together solution for bigger problem. Examples: Closest pair, median selection, quick sort.
• Backtracking: Refinement of brute force search. Build solution incrementally by invoking recursion to try all possibilities for the decision in each step.
• Dynamic Programming: problem reduced to multiple (typically) dependent or overlapping sub-problems. Use memorization to avoid re-computation of common solutions leading to iterative bottom-up algorithm

Backtracking

A backtracking algorithm tries to construct a solution to a computational problem incrementally, one small piece at a time. Whenever the algorithm needs to decide between multiple alternatives to the next component of the solution, it recursively evaluates every alternative and then chooses the best one.

State Tree

A state space tree is a tree constructed from all of the possible states of the problem as nodes, connected via state transitions from some initial state as root to some terminal state as a leaf.

Example 1 - The Queens problem

Problem -

1. How many queens can one place on the board?
2. Can one place 8 queens on the board?

Process:

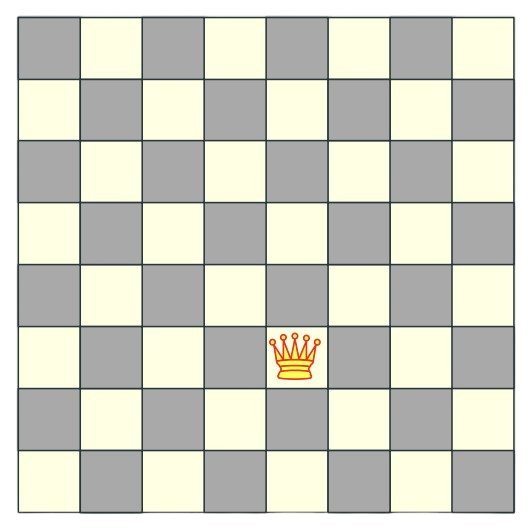
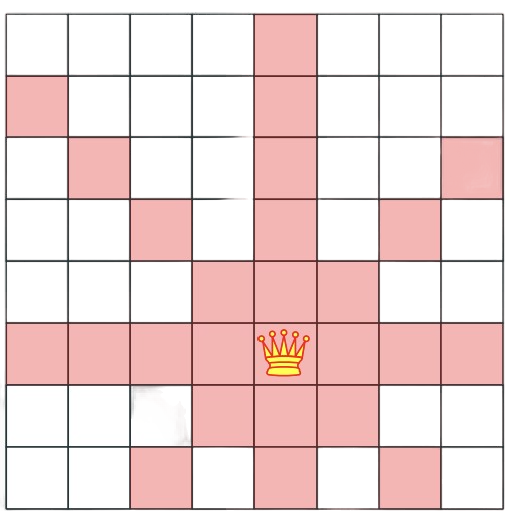
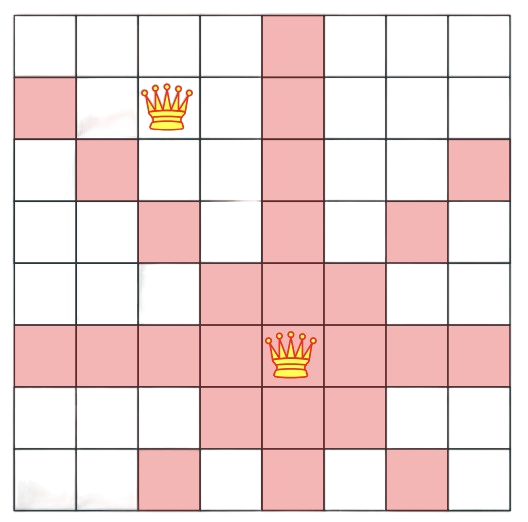
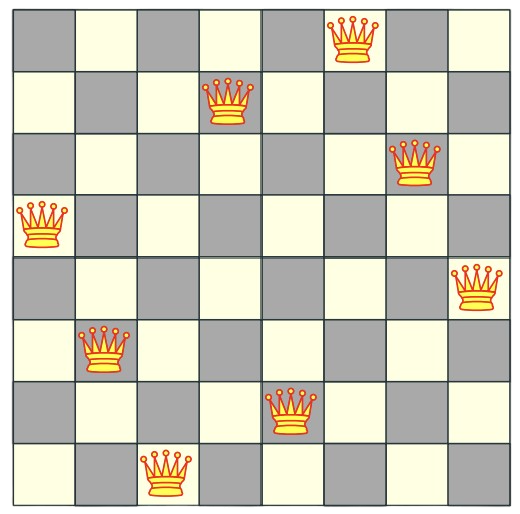
Initial board with Queen 1 placement.	All the possible places that the current queen can go to.	Queen 2 placement.	Final 8-Queen problem solved in 1850 (published in 1848)

Problem :

• How to solve problem for general n?

Intuition:

• Queens can’t be on the same row, column or diagonal
• Can have n queens max.

Search tree for 5 queens:

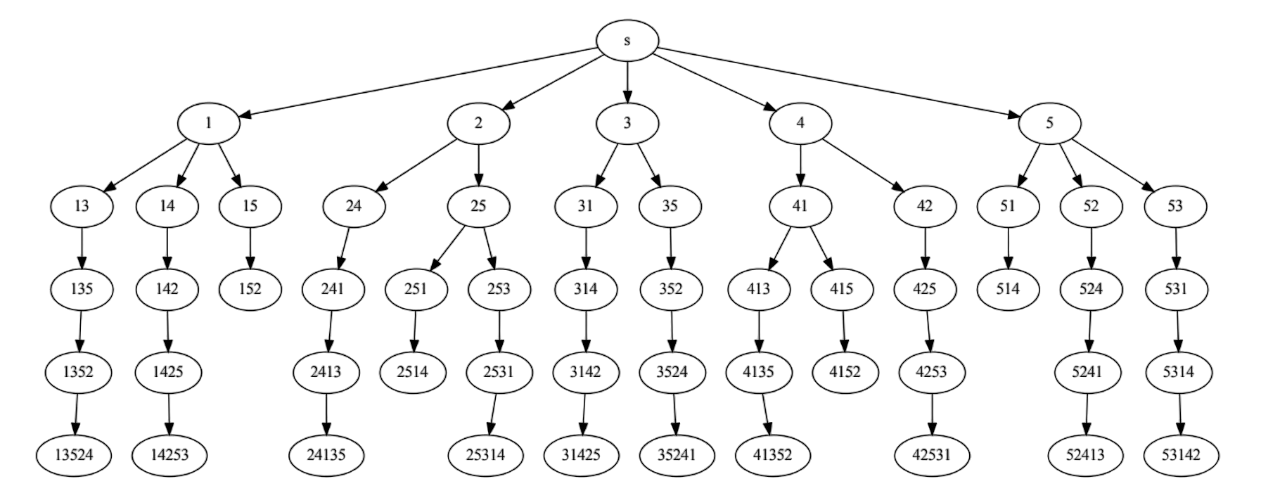
Each node in the state tree represents a board state. For eg. node 135 represents a board where the queens placed on column 1,3 and 5. The leaf nodes represent the final state of the board where either 5 queens are placed or it cannot proceed further.

Hence, we recursively search over an implicit tree, where we “backtrack” if certain possibilities do not work.

Longest Increasing Subsequence (LIS)

Definitions:

• Sequence: an ordered list $a_1$, $a_{2}$,…, $a_{n}$. Length of a sequence is number of elements in the list.
• Subsequence: $a_{i1}$ ,…, $a_{ik}$ is a subsequence of $a_{1}$,…, $a_{n}$ if 1 $\le$ $i_{1}$ < $i_{2}$ <…< $i_{k}$ $\le$ n.
• Increasing sequence: A sequence is increasing if $a_{1}$ < $a_{2}$ <…< $a_{n}$. It is non-decreasing if $a_{1}$ $\le$ $a_{2}$ $\le$ … $\le$ $a_{n}$. Similarly decreasing and non-increasing.

Problem:

• Input: A sequence of numbers $a_{1}$ , $a_{2}$,…, $a_{n}$
• Goal: Find an increasing subsequence $a_{i1}$ , $a_{i2}$ ,…, $a_{ik}$ of maximum length

1. Naive solution:
   

   algLISNaive(A[1..n]):
     max = 0
     for each subsequence B of A do
      if B is increasing and |B| > max then
        max = |B|
     Output max
   

   Running time: O(n$2^n$) for $2^n$ subsequences of a sequence of length n and O(n) time to check if a given sequence is increasing.

2. Recursive solution for LIS(A[1..n]):
   • Case 1: Does not contain A[n] in which case LIS(A[1..n]) = LIS(A[1..(n − 1)])
   • Case 2: Contains A[n] in which case LIS(A[1..n]) is not so clear.
   • Note: For second case we want to find a subsequence in A[1..(n − 1)] that is restricted to numbers less than A[n]. This suggests that a more general problem is LIS_smaller(A[1..n], x) which gives the longest increasing subsequence in A where each number in the sequence is less than x.

LIS_smaller(A[1..n], x):
  if (n = 0) then return 0
  m = LIS_smaller(A[1..(n − 1)], x)
  if (A[n] < x) then
    m = max(m, 1 + LIS_smaller(A[1..(n − 1)], A[n]))
  Output m

LIS(A[1..n]):
  return LIS_smaller(A[1..n], ∞)

Running time: O($2^n$)

General pattern

Backtracking algorithms are commonly used to make a sequence of decisions, with the goal of building a recursively defined structure satisfying certain constraints. Often (but not always) this goal structure is itself a sequence. For example:

• In the n-queens problem, the goal is a sequence of queen positions, one in each row, such that no two queens attack each other. For each row, the algorithm decides where to place the queen.
• In the LIS problem, the goal is a sequence of input elements that have an increasing order of value. For each input element, the algorithm decides whether to include it in the output sequence or not.

Additional Resources

• Textbooks
  • Erickson, Jeff. Algorithms
    • Chapter 3 - Backtracking
  • Skiena, Steven. The Algorithms Design Manual
    • Chapter 9.1 - Backtracking
    • Chapter 9.2 - Examples of sBacktracking
• Sariel’s Lecture 12