Directed Acyclic Graph
Definition
A directed graph G is a directed acyclic graph (DAG) if there is no directed cycle in G.
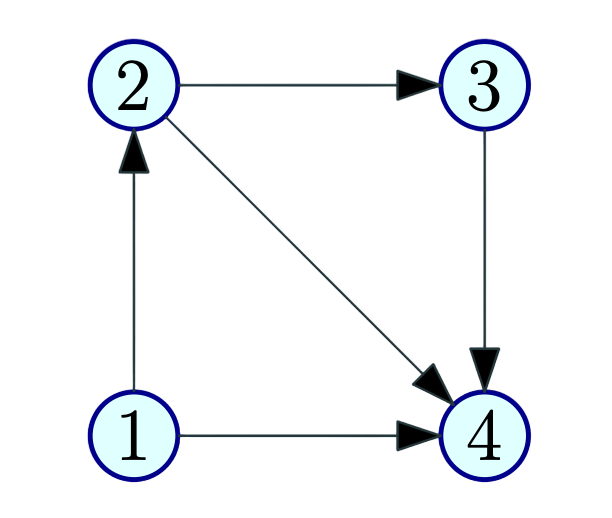
- A vertex u is a source if it has no in-coming edges.
- A vertex u is a sink if it has no out-going edges.
Properties
- Every DAG G has at least one source and at least one sink
- G is a DAG if and only if $G^{rev}$ is a DAG
- G is a DAG if and only if each node is in its own strong connected component
Topological Ordering/Sorting
Definition
A topological ordering/topological sorting of G = (V, E) is an ordering $<$ on V such that if $(u → v) \in E $ then $u < v$ .
Informal Definition : One can order the vertices of the graph along a line (say the x-axis) such that all edges are from left to right.
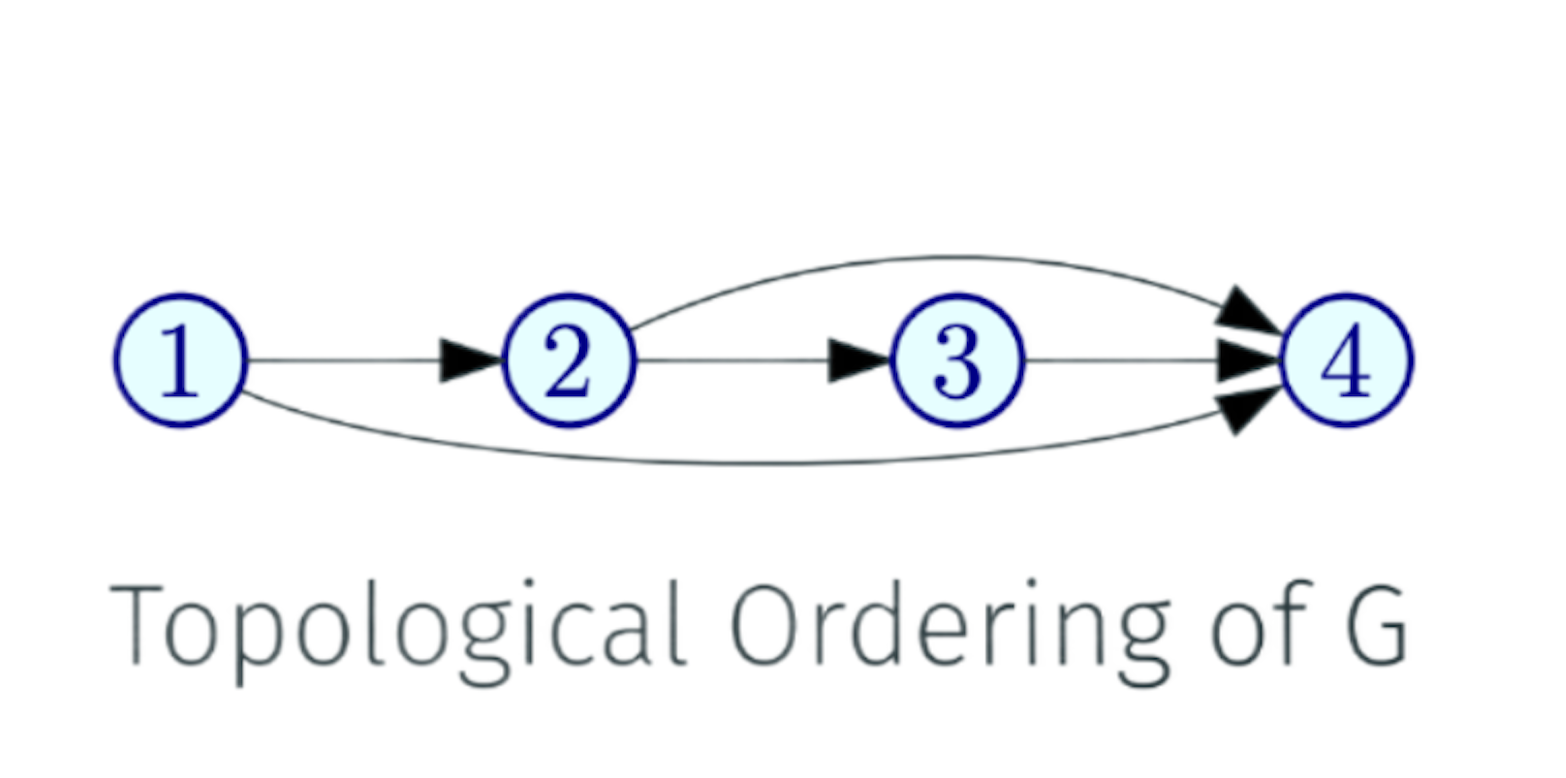
- A DAG G may have many different topological sorts
- A directed graph G can be topologically ordered if G is a DAG
- A directed graph G is a DAG if G can be topologically ordered
Depth First Search
DFS with pre-post numbering in directed graphs
The Pre-visit number indicates when the node enters the DFS recursion stack, and the Post-visit number indicates when the node exits the DFS recursion stack. Pre and Post numbers can be used to determine whether a particular node is in the sub-tree of another node.
DFS(G)
Mark all nodes u as unvisited
T is set to ∅
time = 0
while there is an unvisited node u do
DFS(u)
Output T
DFS(u)
Mark u as visited
pre(u) = ++time
for each edge (u, v) in Out(u) do
if v is not visited
add edge (u, v) to T
DFS(v)
post(u) = ++time
Properties
- Node u is active in time interval [pre(u), post(u)]
- DFS(G) takes O(m + n) time
- Edges added form a branching: a forest of out-trees
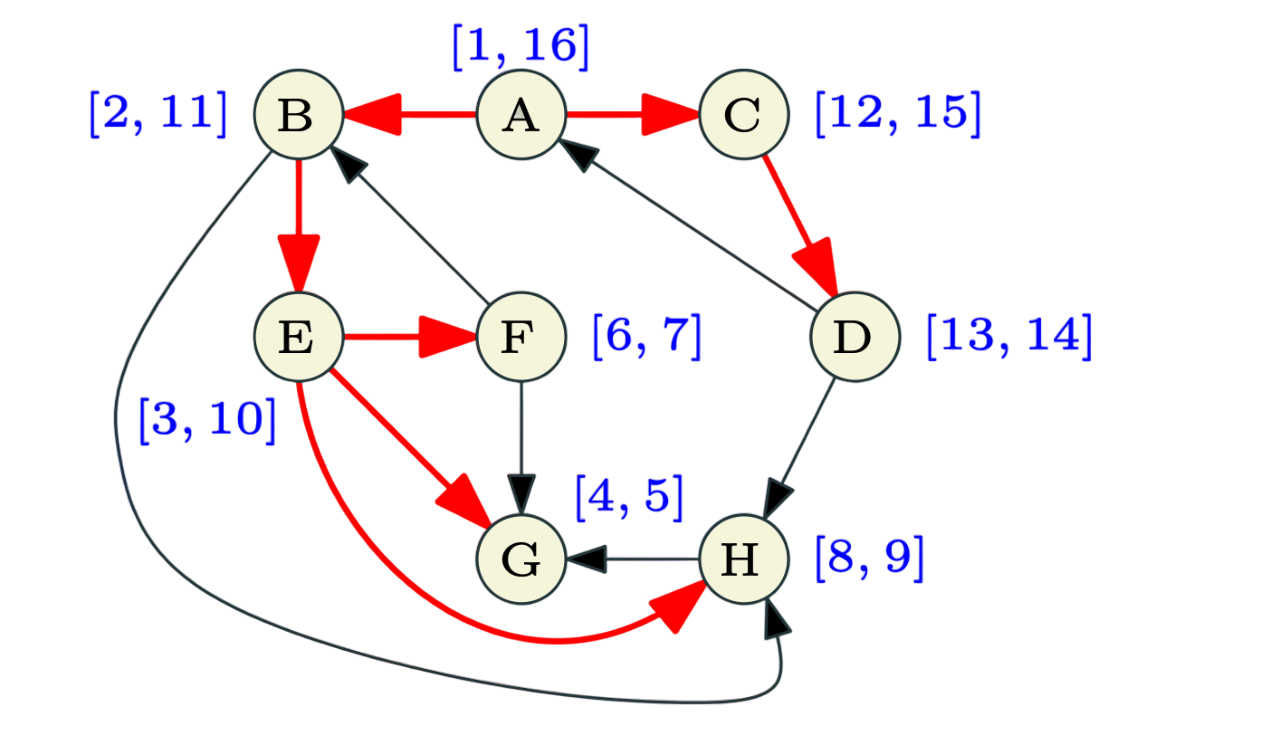
- For any two nodes u and v, the two intervals [pre(u), post(u)] and [pre(v), post(v)] are disjoint or one is contained in the other
- To find whether u lies in the sub-tree of v or not we just compare the pre and post number of u and v. If $pre[u] > pre[v]$ and $post[u] < post[v]$ then u lies in the sub-tree of v otherwise not.
- Output of DFS(G) depends on the order in which vertices are considered
- If u is the first vertex considered by DFS(G) then DFS(u) outputs a directed out-tree T rooted at u and a vertex v is in T if and only if $v ∈ rch(u)$
Example
Edges of G can be classified with respect to the DFS tree T as:
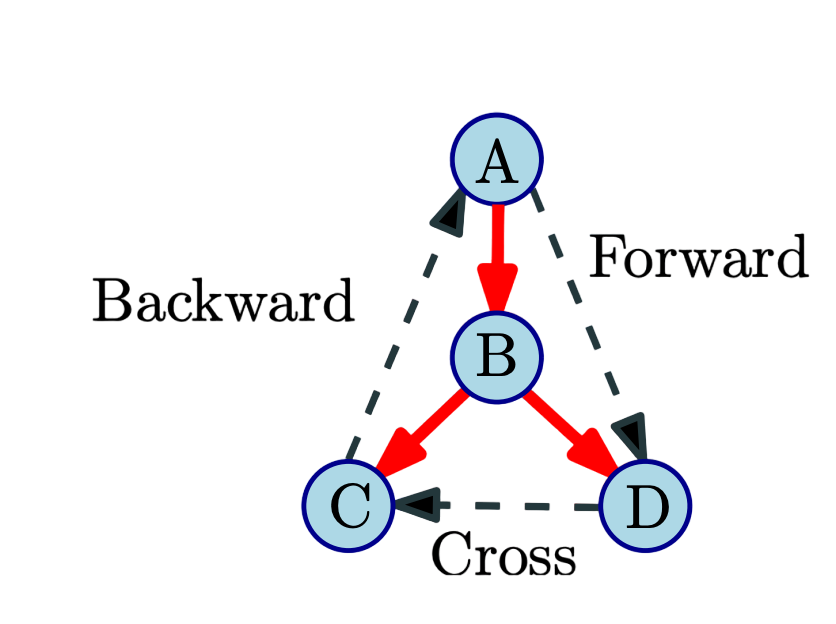
- Tree edges that belong to T
- A forward edge is a non-tree edges (x, y) such that y is a descendant of x i.e, $pre(x) < pre(y) < post(y) < post(x)$.
- A backward edge is a non-tree edge (x, y) such that y is an ancestor of x.
- A cross edge is a non-tree edges (x, y) such that they don’t have a ancestor/descendant relationship between them.
Cycle detection in directed graph using topological sorting
Given a graph G, if it is a Directed Acyclic graph then compute a topological sort. If it failes, then output the cycle C.
The algorithm will be as follows:
- Compute DFS(G)
- If there is a back edge e = (v, u) then G is not a DAG. Output cycle C formed by path from u to v in T plus edge (v, u).
- Otherwise output nodes in decreasing post-visit order.
The above algorithm runs in $O(n + m)$ time.
Graph of strong connected components
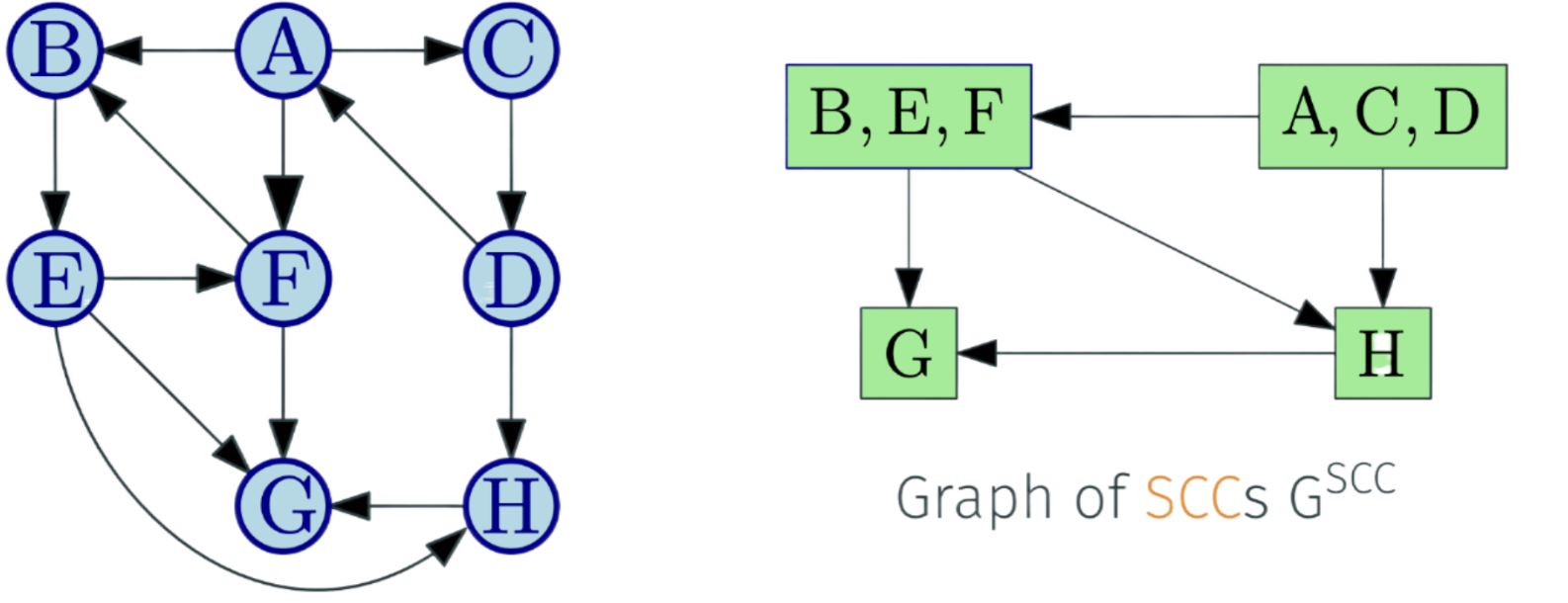
Let $S_1, S_2, . . . S_k$ be the strong connected components (i.e.,SCCs) of G. The graph of SCCs is $G^{SCC}$. It is created by collapsing every strong connected component to a single vertex.
- Vertices are $S_1, S_2, . . . S_k$
- There is an edge $(S_i, S_j)$ if there is some $u \in S_i$ and $v \in S_j$ such that (u, v) is an edge in G
For a directed graph G, its meta-graph $G^{SCC}$ is a DAG.
The straightforward algorithm(discussed in Lecture 15) to find all SCCs of a given directed graph has a running time of $O(n(n + m))$.
The Linear time Algorithm for SCCs will be as follows:
- Let u be a vertex in a sink SCC of $G^{SCC}$
- Do DFS(u) to compute SCC(u)
- Remove SCC(u) and repeat
If v is the vertex with maximum post numbering in $DFS(G^{rev})$. Then v is in a SCC S, such that S is a sink of $G^{SCC}$. So, we can find a vertex in a sink SCC of $G^{SCC}$ for the linear time algorithm. Let us assume $G1=G^{rev}$.
do DFS(G1) and output vertices in decreasing post order.
Mark all nodes as unvisited
for each u in the computed order do
if u is not visited then
DFS(u)
Let S1 be the nodes reached by u
Output S1 as a strong connected component
Remove S1 from G
The above algorithm runs in time $O(m + n)$ and correctly outputs all the SCCs of G.
Additional Resources
- Textbooks
- Erickson, Jeff. Algorithms
- Skiena, Steven. The Algorithms Design Manual
- Chapter 7.8 - Depth-First Search
- Chapter 7.9 - Applications of Depth-First Search
- Chapter 7.10 - Depth-First Search on Directed Graphs
- Sedgewick, Robert and Wayne, Kevin. Algorithms (Forth Edition)
- Chapter 4.2 - Directed Graphs
- Cormen, Thomas, et al. Algorithms (Forth Edition)
- Chapter 20.3 - Depth-First Search
- Chapter 20.4 - Topological Sort
- Sariel’s Lecture 16
- Jeff’s - Notes on Depth-First Search

